Question

Две окружности, расстояние между центрами которых равно 21, а радиусы равны 13 и 20, пересекаются в точках P и Q. На меньшей из этих окружностей взята точка L так, что прямая LQ касается большей окружности. Найдите площадь треугольника LPQ.

Помогите решить, пожалуйста!) Желательно с рисунком. Даю 50 баллов.

Answer 1

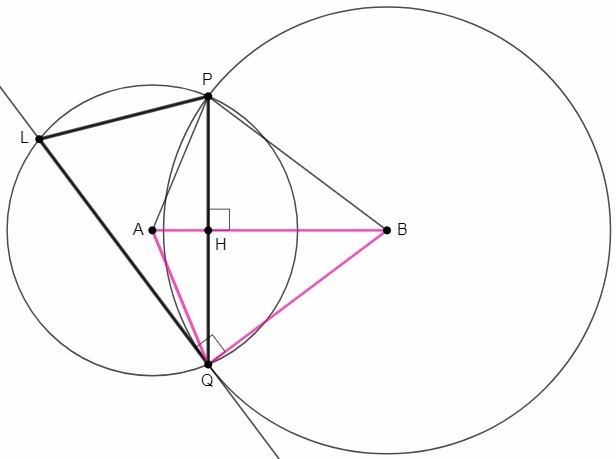
∪PQ - дуга окружности c центром B (большей)
∪PQ' - дуга окружности c центром A

△APB=△AQB (по трем сторонам)
∠ABP=∠ABQ, ∠PAB=∠QAB

Угол между касательной и хордой, проведенной в точку касания, равен половине дуги, стягиваемой хордой.
∠LQP=∪PQ/2
Центральный угол равен дуге, на которую опирается.
∠PBQ=∪PQ
∠ABQ=∠PBQ/2 =∪PQ/2 =∠LQP

∠PAQ=∪PQ'
∠QAB=∠PAQ/2=∪PQ'/2
Вписанный угол равен половине дуги, на которую опирается.
∠PLQ=∪PQ'/2=∠QAB

△LPQ~△AQB (по двум углам)

△PBQ - равнобедренный, BH - биссектриса, высота, медиана.
PQ⊥AB, PH=QH

AB=21, QA=13, QB=20
По формуле Герона
p= (13+20+21)/2 =27
S(AQB)= √(p(p-a)(p-b)(p-c)) =√(27*14*7*6) =3*3*7*2 =126

S(AQB)=AB*QH/2 <=> 126=21*QH/2 <=> QH=12
PQ=2QH =24

k=PQ/QB =24/20 =1,2

Площади подобных треугольников относятся как квадрат коэффициента подобия.
S(LPQ)= S(AQB)*k^2 =126*1,44 =181,44

Answer 2

ПОМОГИТЕ ПОЖАЛУЙСТА
https://znanija.com/task/29216184