Высота правильной четырехугольной пирамиды = 3 см, а сторона ее основания - 12 см. Найдите длину бокового ребра пирамиды!
Приложения:

Ответы
Ответ дал:
0
Я использовала теорему Пифагора
Приложения:
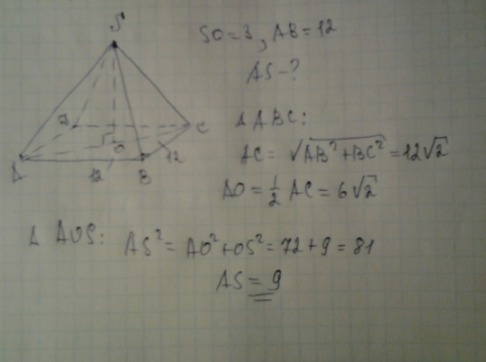
Ответ дал:
0
Дано:правильная четырехугольная пирамида АВСDEF
где ЕF-высота равна 3см
АВСD-основание а=12см
Найти боковую сторону
Решение:
На стороне основания ставим точку G так чтобы АG=GD
от точки G строим отрезом GF
GF=1/2 AB
GF=6 см
Рассмотрим треугольник GFE
GF=6 FE=3
GD-гипотенуза, ее длину находим по теореме пифагора
c^2=a^2+b^2
GE^2=GF^2+FE^2=6^2+3^2=36+9=45см^2
GE=√45=√(9*5)=3√5см
Ответ:3√5см
где ЕF-высота равна 3см
АВСD-основание а=12см
Найти боковую сторону
Решение:
На стороне основания ставим точку G так чтобы АG=GD
от точки G строим отрезом GF
GF=1/2 AB
GF=6 см
Рассмотрим треугольник GFE
GF=6 FE=3
GD-гипотенуза, ее длину находим по теореме пифагора
c^2=a^2+b^2
GE^2=GF^2+FE^2=6^2+3^2=36+9=45см^2
GE=√45=√(9*5)=3√5см
Ответ:3√5см
Приложения:

Ответ дал:
0
Можешь нарисовать ?
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад