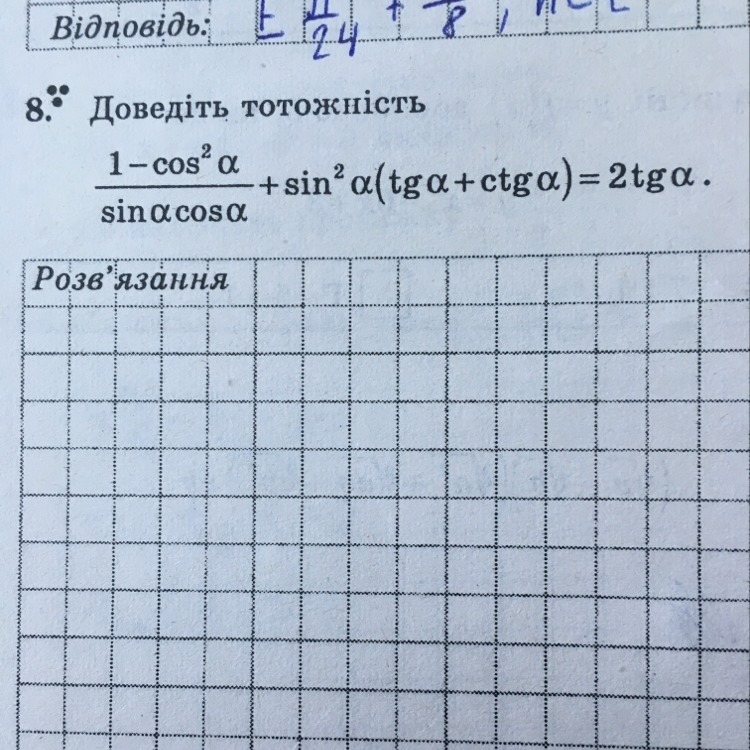Question

Математика 10 класс. Довести тотожність

Answer 1

1-(cosx)^2/sinxcosx + (sinx)^2(tgx + ctgx)=2tgx
(sinx)^2/sinxcosx + (sinx)^2(tgx + ctgx)=2tgx
sinx/cosx + (sinx)^2(tgx + ctgx)=2tgx
tgx + (sinx)^2(tgx + ctgx)=2tgx
(sinx)^2(tgx + ctgx)=2tgx - tgx
(sinx)^2(tgx + ctgx)=tgx
(sinx)^2(tgx/tgx + ctgx/tgx)=tgx/tgx
(sinx)^2(1 + ctgx/tgx)=1 
отдельно ctgx/tgx= sinx/cosx/cosx/sinx=sinxsinx/cosxcosx =(sinx)^2/(cosx)^2

(sinx)^2(1 + (sinx)^2/(cosx)^2)=1
(sinx)^2(((cosx)^2 + (sinx)^2)/(cosx)^2)=1
(sinx)^2(1/(cosx)^2)=1
(tgx)^2=1
tgx = 1 
tgx = -1
ответ
х1 = П/4 +Пк х пренад z
x2 = -П/4 + Пк х пренад z

Answer 2

$displaystylemathtt{frac{1-cos^2alpha}{sinalpha cosalpha}=frac{sin^2alpha}{sinalpha cosalpha}=frac{sinalpha}{cosalpha}=tgalpha}$, следовательно, 

$displaystylemathtt{frac{1-cos^2alpha}{sinalpha cosalpha}+sin^2alpha(tgalpha+ctgalpha)=sin^2alpha(tgalpha+ctgalpha)=tgalpha}$

поделив на тангенс обе части уравнения, теперь нам необходимо доказать новое тождество: $displaystylemathtt{frac{sin^2alpha(tgalpha+ctgalpha)}{tgalpha}=1}$

$displaystylemathtt{frac{sin^2alpha(tgalpha+ctgalpha)cosalpha}{sinalpha}=sinalpha(tgalpha+ctgalpha)cosalpha=}\\mathtt{sinalpha cosalpha tgalpha+sinalpha cosalpha ctgalpha=sin^2alpha+cos^2alpha=1}$