Найти общее решение системы дифференциального уравнения и выделить частное решение, удовлетворяющее начальным
условиям
Приложения:
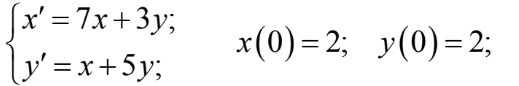
Ответы
Ответ дал:
0
Продифференцируем первое уравнение, имеем
 и
и 
Подставляем все эти данные во второе уравнение, получим

последнее уравнение является дифференциальным уравнением с постоянными коэффициентами, однородным уравнение.
Пусть , тогда получим характеристическое уравнение:
, тогда получим характеристическое уравнение:


Тогда

Найдем теперь частное решение, подставляя начальные условия

Частное решение: и
и 
Подставляем все эти данные во второе уравнение, получим
последнее уравнение является дифференциальным уравнением с постоянными коэффициентами, однородным уравнение.
Пусть
Тогда
Найдем теперь частное решение, подставляя начальные условия
Частное решение:
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад