Question

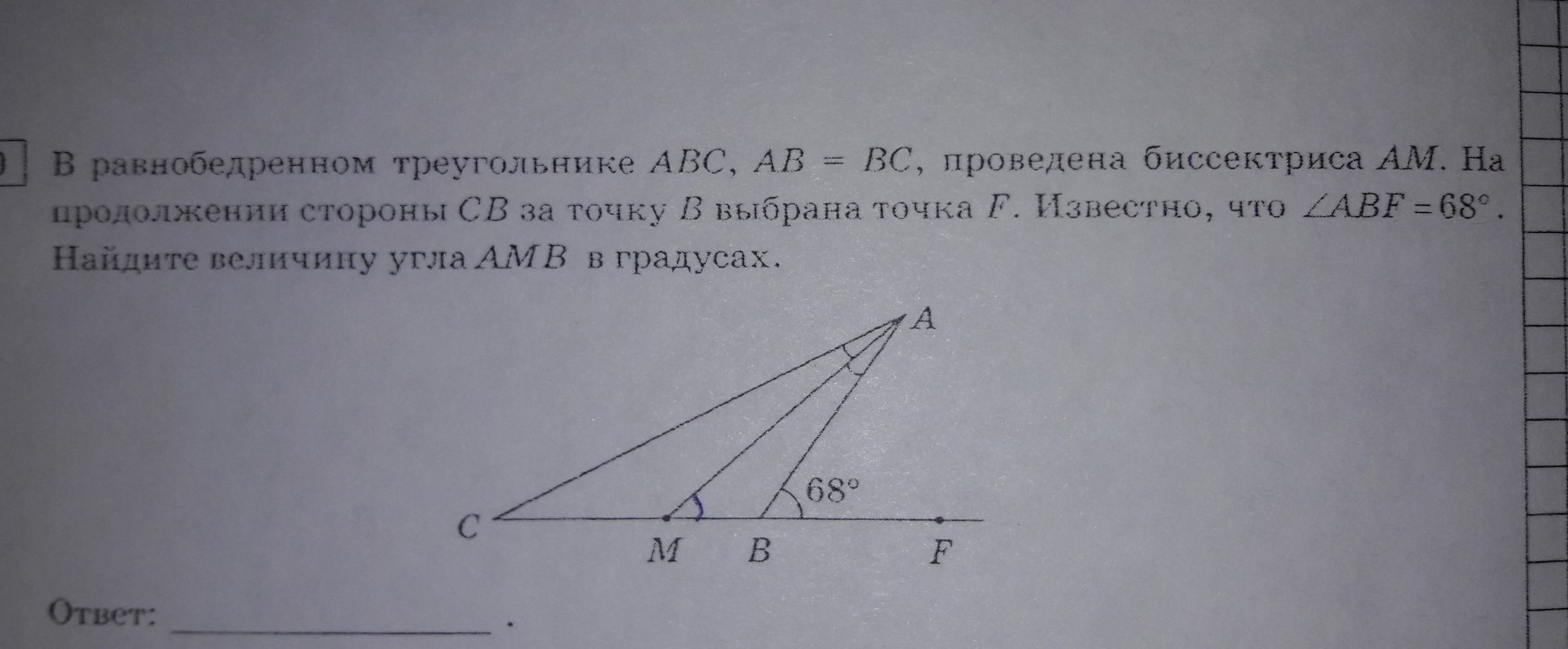
в равнобедренном треугольнике ABC, AB=BC, проведена биссектриса АМ. На продолжении стороны AB за точку B выбрана точка f известно,что Угол ABC =68 градусов.Найдите величину угла acb в градусах

Answer 1

ΔABC :  ∠ABF - внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним  ⇒
∠ACB + ∠CAB = ∠ABF = 68°

Так как треугольник ΔABC равнобедренный по условию (AB=BC, AC - основание), то   ∠ACB = ∠CAB = 68°/2 = 34°

AM - биссектриса ∠САВ  ⇒
∠CAM = ∠BAM = 34°/2 = 17°

ΔAMB : ∠ABF - внешний угол треугольника  ⇒
∠AMB + ∠BAM = ∠ABF
∠AMB + 17° = 68°
∠AMB = 51°

Ответ: ∠AMB = 51°