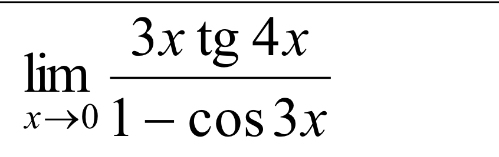Ответы
Ответ дал:
0
Это не уравнение, а предел.
![[frac{0}{0} ] = lim_{x to 0} frac{(3x cdot tg(4x))'}{(1-cos(3x))'} = [frac{0}{0} ] = lim_{x to 0} frac{(3x cdot tg(4x))'}{(1-cos(3x))'} =](https://tex.z-dn.net/?f=%5Bfrac%7B0%7D%7B0%7D+%5D+%3D++lim_%7Bx+to+0%7D+frac%7B%283x+cdot+tg%284x%29%29%27%7D%7B%281-cos%283x%29%29%27%7D++%3D+)
![lim_{x to 0} frac{ 3tg(4x) + frac{12x}{(cos(4x))^2} }{ 3sin(3x) } = [ frac{0}{0} ] = lim_{x to 0} frac{ (3tg(4x) + frac{12x}{(cos(4x))^2})' }{ 3sin(3x)' } = lim_{x to 0} frac{ 3tg(4x) + frac{12x}{(cos(4x))^2} }{ 3sin(3x) } = [ frac{0}{0} ] = lim_{x to 0} frac{ (3tg(4x) + frac{12x}{(cos(4x))^2})' }{ 3sin(3x)' } =](https://tex.z-dn.net/?f=+lim_%7Bx+to+0%7D+frac%7B+3tg%284x%29+%2B+frac%7B12x%7D%7B%28cos%284x%29%29%5E2%7D+%7D%7B+3sin%283x%29+%7D+%3D+%5B+frac%7B0%7D%7B0%7D+%5D+%3D+lim_%7Bx+to+0%7D+frac%7B+%283tg%284x%29+%2B+frac%7B12x%7D%7B%28cos%284x%29%29%5E2%7D%29%27+%7D%7B+3sin%283x%29%27+%7D+%3D+)

Ответ дал:
0
Чем, собственно, не устроил ответ?
Вас заинтересует
2 года назад
3 года назад
9 лет назад
10 лет назад
10 лет назад