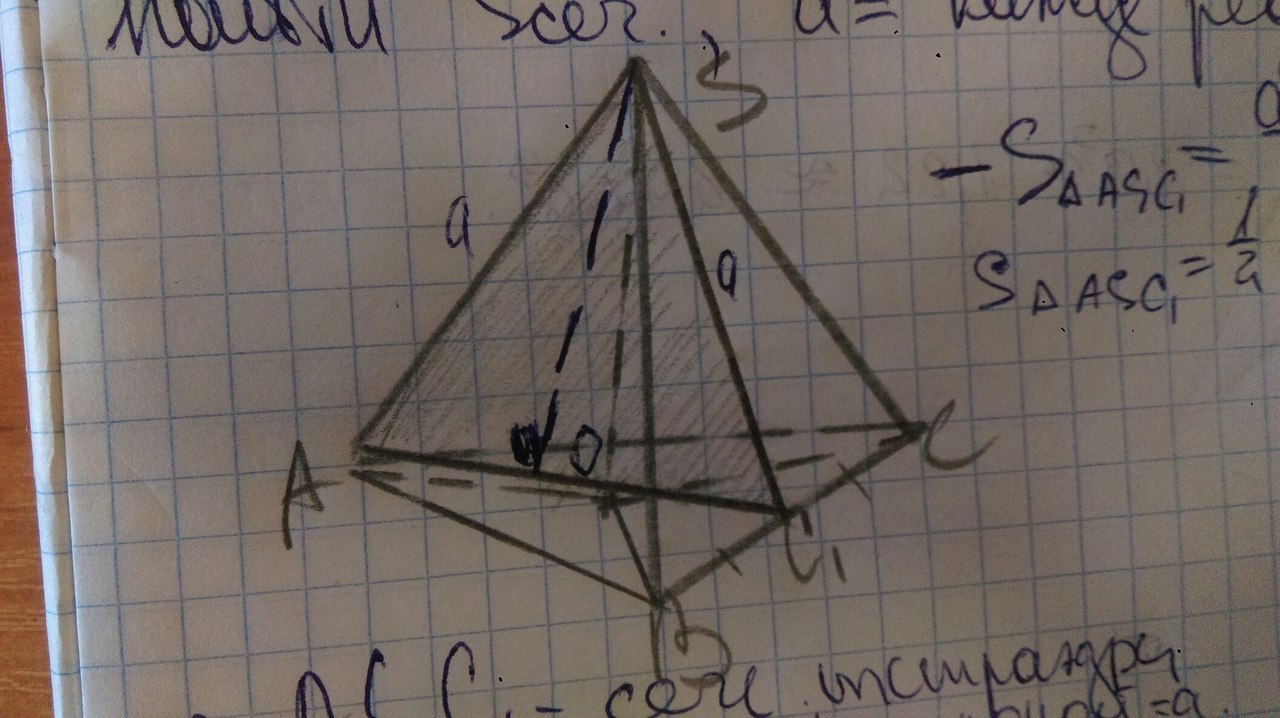
построить площадь сечения тетраэдра SABC плоскостью,проходящей через ребро SA и точку пересечения медиан ABC.Найти площадь сечения,каждое ребро сечения равно а.Сечения построено,нужно найти только площадь сечения
Приложения:

Ответы
Ответ дал:
0
В правильном тетраэдре заданное сечение - это осевое сечение через боковое ребро, равное а.
В сечении - равнобедренный треугольник, 2 стороны которого - апофемы А.
Апофема А = a*cos30° = a√3/2.
Высота h к стороне а равна √((а√3/2)²-(а/2)²) = а√2/2.
Тогда площадь сечения S = (1/2)ah = (1/2)a*(a√2/2) = a²√2/4.
В сечении - равнобедренный треугольник, 2 стороны которого - апофемы А.
Апофема А = a*cos30° = a√3/2.
Высота h к стороне а равна √((а√3/2)²-(а/2)²) = а√2/2.
Тогда площадь сечения S = (1/2)ah = (1/2)a*(a√2/2) = a²√2/4.
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад
10 лет назад