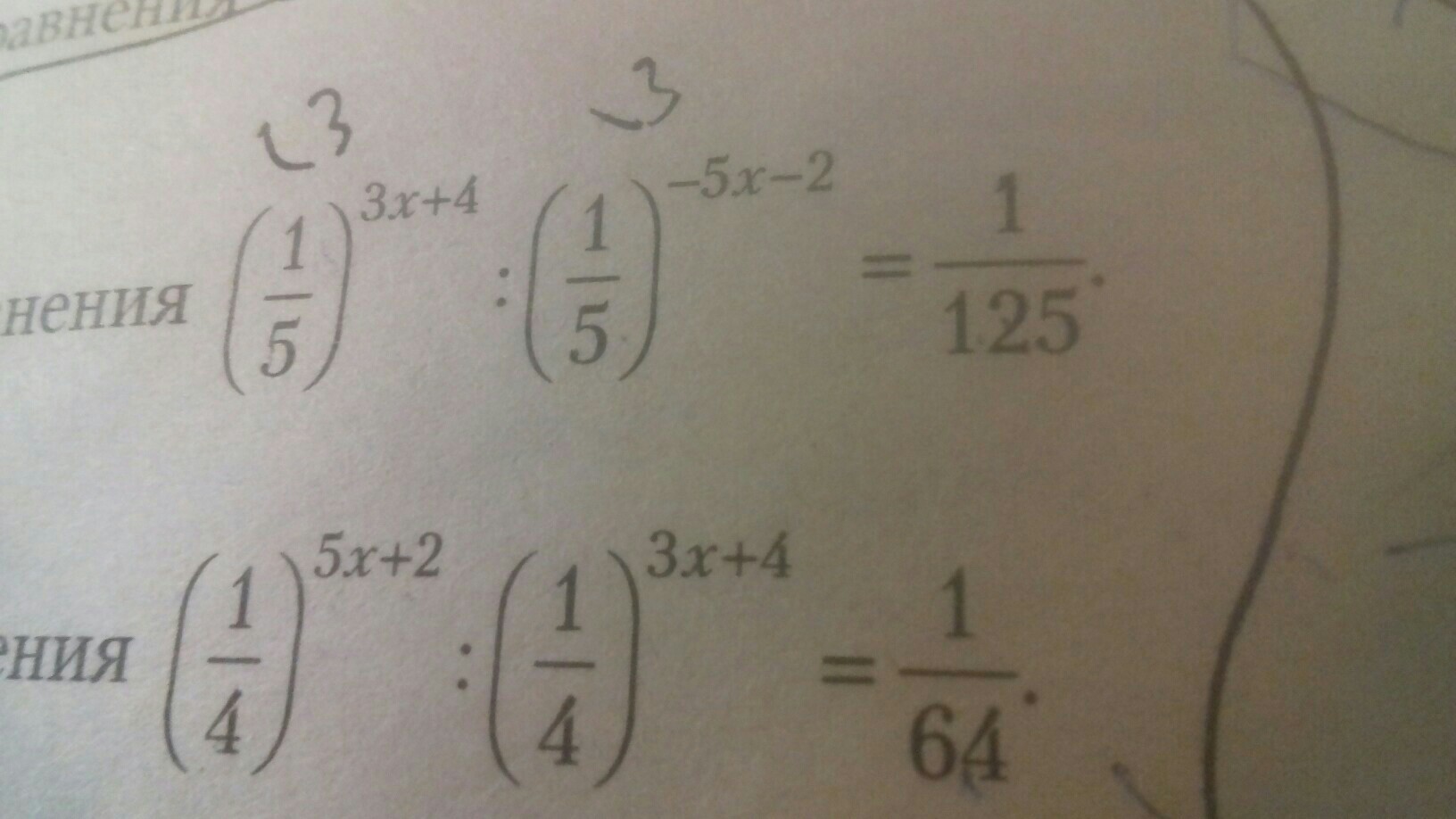Question

Решите оба, пожалуйста

Answer 1

(1/5)^3x+4:(1/5)^-5x-2=1/125
(1/5)^3x+4:(1/5)^-5x-2=1/125
(1/5)^8x+6=5^-3
5^-(8x+6)=5^-3
5^-8x-6=^-3
-8x-6=-3
-8x-6=-3+6
-8x=3
x=-3/8

(1/4)^5x+2:(1/4)^3x+4=1/64
(1/64)^5x+2:(1/4)^3x+4=1/64
(1/4)^2x-2=2^-6
2^-4x+4=2^-6
-4x+4=-6
-4x=-6-4
-4x=-10
x=2,5

Answer 2

Спасибо, сейчас исправлю

Answer 3

PamPam, обновите страницу

Answer 4

Поскольку основания одинаковы, нужно приравнять показатели

Answer 5

5^-8х-6=5^-3

Answer 6

а, все понятно. спасибо!))

Answer 7

$( frac{1}{5} )^{3x+4}:( frac{1}{5} )^{-5x-2}= frac{1}{125} \ \ ( frac{1}{5} )^{3x+4-(-5x-2)}= frac{1}{5^3} \ \ ( frac{1}{5} )^{8x+6}= (frac{1}{5})^3 \ \ 8x+6=3 \ 8x=3-6 \ 8x=-3 \ x=- frac{3}{8} \ \ \ ( frac{1}{4} )^{5x+2}:( frac{1}{4} )^{3x+4}= frac{1}{64} \\ ( frac{1}{4} )^{5x+2-(3x+4)}= frac{1}{4^3}\\ ( frac{1}{4} )^{2x-2}= (frac{1}{4})^3 \ \ 2x-2=3 \ 2x=3+2 \ 2x=5 \ x=2.5$

Answer 8

у вас 2 степени с одинаковыми показателями, основание остается прежним (1/5), показатели вычитаем:

Answer 9

спасибо! :))

Answer 10

3х+4-(-5х-2) = 3х+4+5х+2 = 8х+6

Answer 11

да, все понятно) Спасибо)

Answer 12

пожалуйста)