Ответы
Ответ дал:
0
Найти площадь фигуры, ограниченной линиями
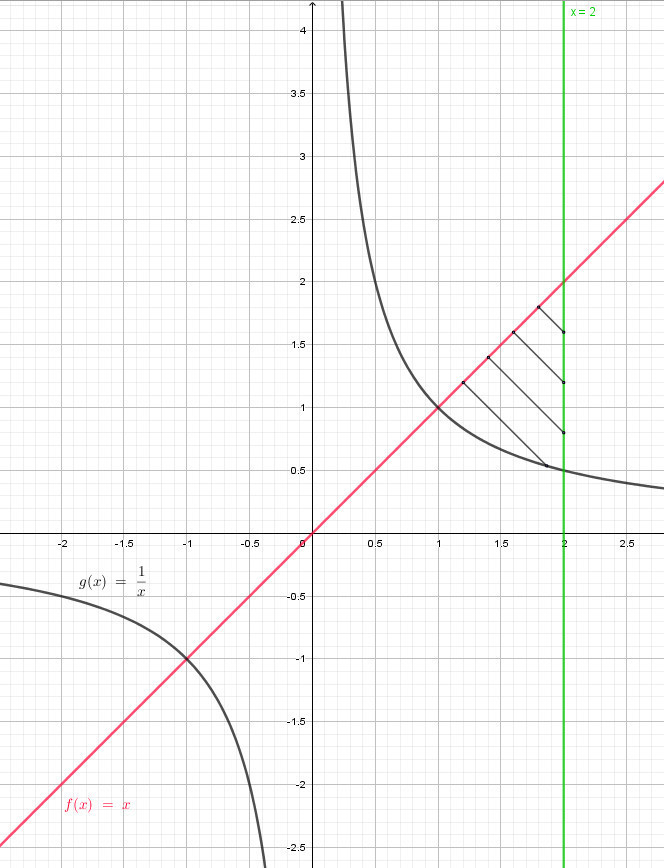
y=1/x; y=x; x=2
Решение
Построим в системе координат xOy эти линии. Найдем точки пересечения этих линий.

x = 1/x
x - 1/x = 0
(x²-1)/x = 0
x² = 1
x₁ = -1; x₂ = 1
y₁= -1; y₂ = 1
График функций приведен во вложении
Замкнутая область площадь которой надо найти ограничена сверху функцией y = x и снизу функцией y =1/x. Интервал интегрирования 1≤x≤2
![S= intlimits^2_1 {(x- frac{1}{x}) } , dx= (frac{x^2}{2}-ln|x|) left[begin{array}{c}2\1end{array}right]= frac{2^2}{2}-ln|2|- frac{1}{2}+ln|1|= S= intlimits^2_1 {(x- frac{1}{x}) } , dx= (frac{x^2}{2}-ln|x|) left[begin{array}{c}2\1end{array}right]= frac{2^2}{2}-ln|2|- frac{1}{2}+ln|1|=](https://tex.z-dn.net/?f=S%3D+intlimits%5E2_1+%7B%28x-+frac%7B1%7D%7Bx%7D%29+%7D+%2C+dx%3D+%28frac%7Bx%5E2%7D%7B2%7D-ln%7Cx%7C%29++left%5Bbegin%7Barray%7D%7Bc%7D2%5C1end%7Barray%7Dright%5D%3D+frac%7B2%5E2%7D%7B2%7D-ln%7C2%7C-+frac%7B1%7D%7B2%7D%2Bln%7C1%7C%3D++++)

S=0,807
Ответ:0,807
y=1/x; y=x; x=2
Решение
Построим в системе координат xOy эти линии. Найдем точки пересечения этих линий.
x = 1/x
x - 1/x = 0
(x²-1)/x = 0
x² = 1
x₁ = -1; x₂ = 1
y₁= -1; y₂ = 1
График функций приведен во вложении
Замкнутая область площадь которой надо найти ограничена сверху функцией y = x и снизу функцией y =1/x. Интервал интегрирования 1≤x≤2
S=0,807
Ответ:0,807
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад