Question

наклонная образует с плоскостью угол 45. длина перпендикуляра равна 8 найти длину наклонной и её проекции на данную плоскость

Answer 1

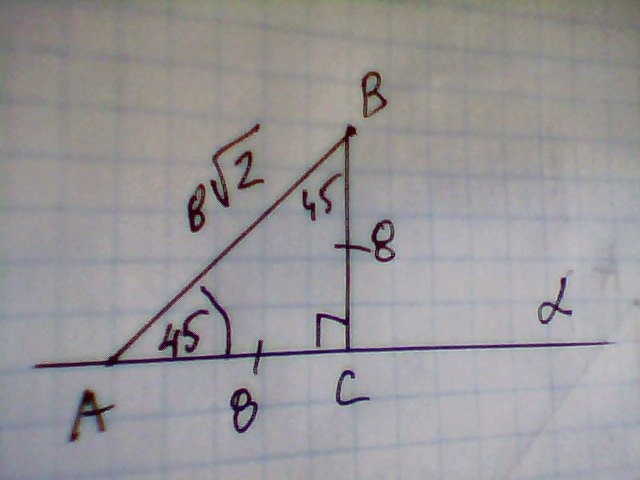
Плоскость α изображена ввиде прямой, Наклонная АВ=8. по условию 
∠ВАС=45°, ВС=8.
ΔАВС- прямоугольный равробедренный, ∠ВАС=АВС=45°, АС=ВС=8
Прекция равна 8, определим длину наклонной по теорему Пифагора.
АВ²=АС²+ВС²=64+64=128.
АВ=√128=8√2.