Знайдіть найменше значення виразі x^2+5y^2+4xy-4y+4.При яких значення змінних він його приймає ?
Ответы
Ответ дал:
0
Найменше значення 0. Коли х=4, у=2. Див. Додаток.
Приложения:
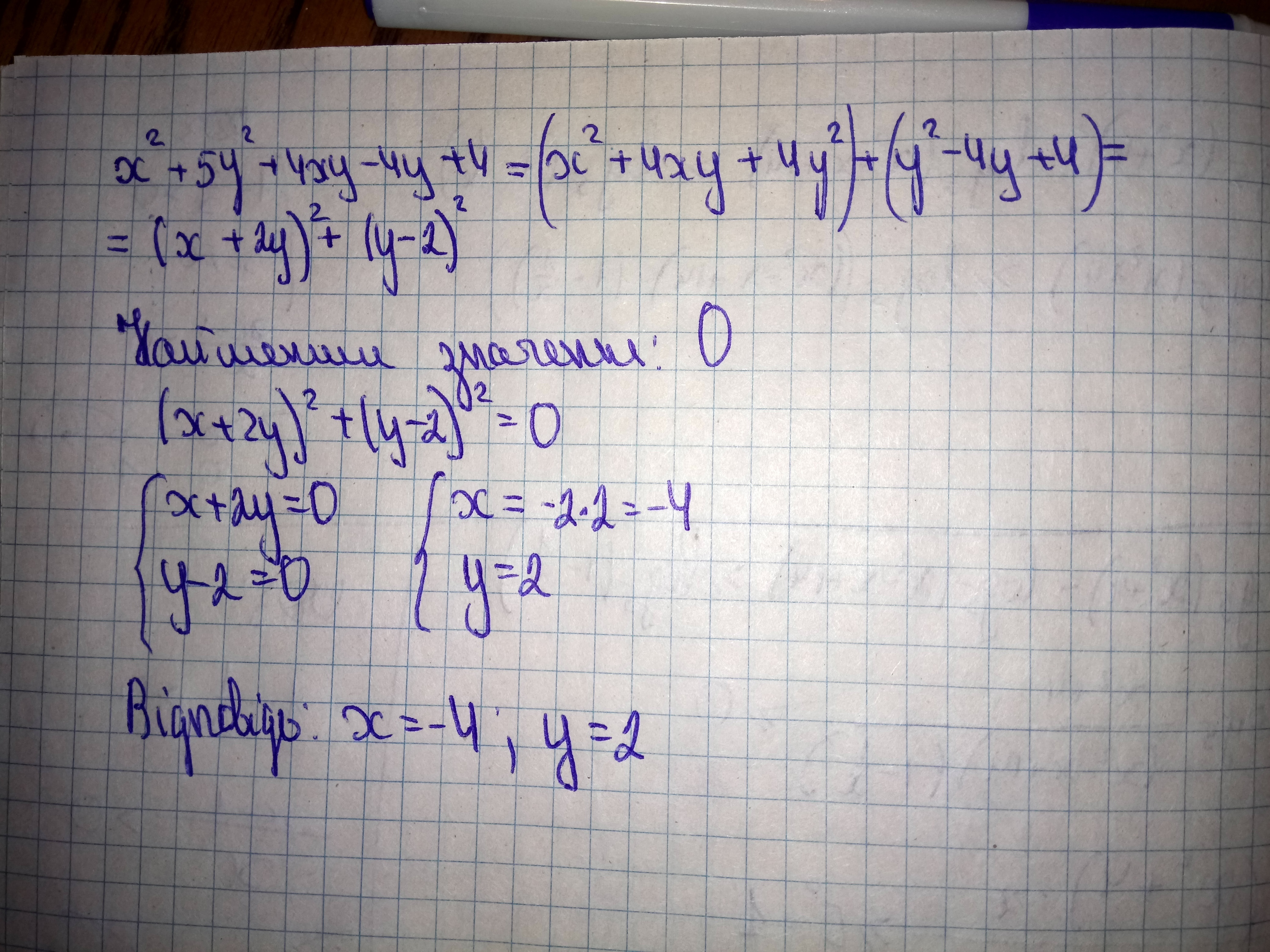
Ответ дал:
0
x²+5y²+4xy-4y+4=x²+4xy+4y²+y²-4y+4=(x+2y)²+(y-2)²
Наименьшее значение такого выражения не может быть меньше нуля, т.к. суммируются числа в квадрате. Следовательно, наименьшее значение будет нулем, остается лишь найти значения переменных. Оба числа должны равняться нулю.
Сначала определим значение переменной у, затем подставим ее, чтобы найти х.
(y-2)²=0
y=2
(x+2y)²=0
y=2 ⇒ (x+4)²=0
x=-4
Ответ: Наименьшее значение выражения 0, при значениях переменных x=-4; y=2.
Наименьшее значение такого выражения не может быть меньше нуля, т.к. суммируются числа в квадрате. Следовательно, наименьшее значение будет нулем, остается лишь найти значения переменных. Оба числа должны равняться нулю.
Сначала определим значение переменной у, затем подставим ее, чтобы найти х.
(y-2)²=0
y=2
(x+2y)²=0
y=2 ⇒ (x+4)²=0
x=-4
Ответ: Наименьшее значение выражения 0, при значениях переменных x=-4; y=2.
Приложения:
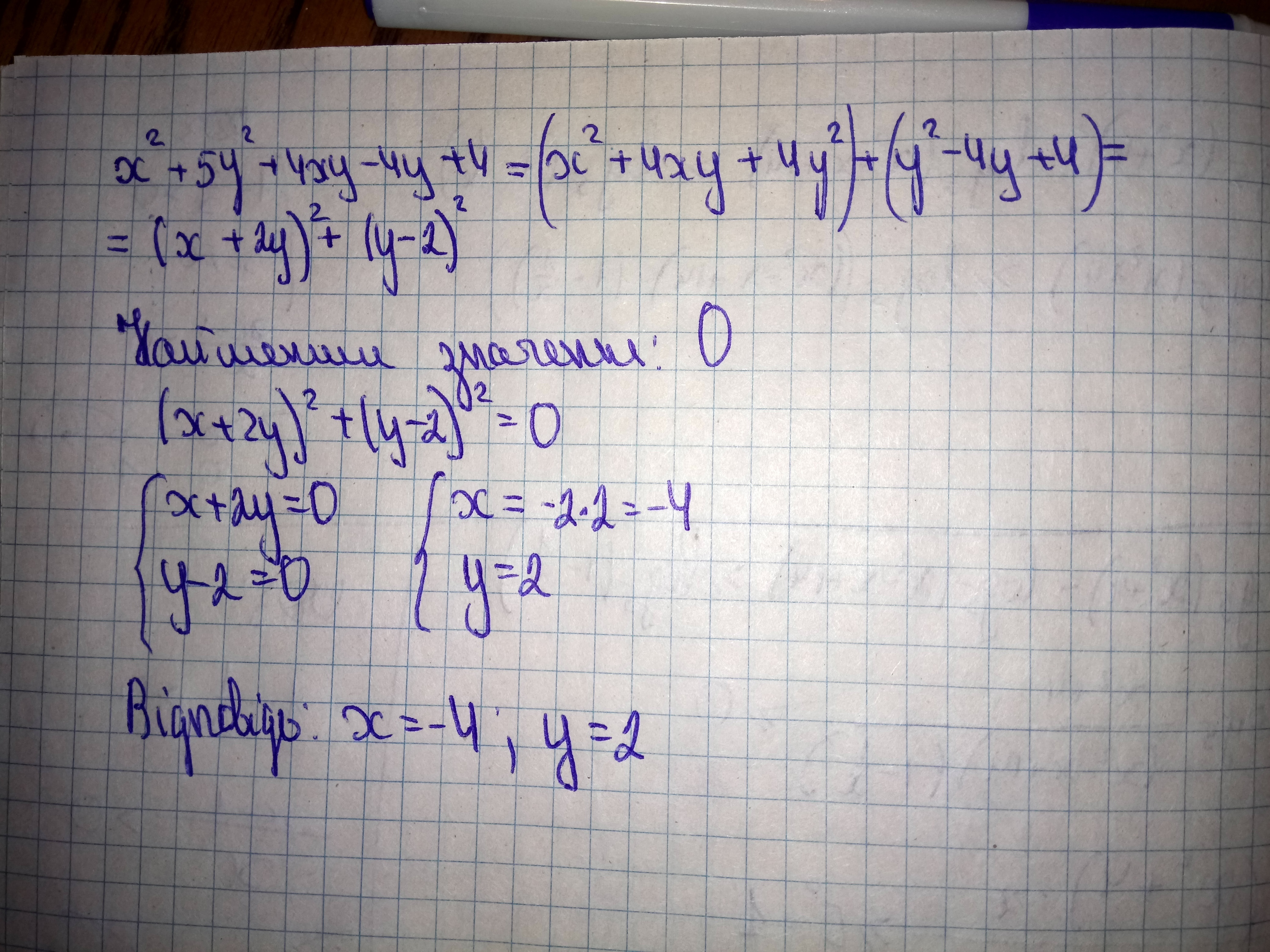
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад