Question

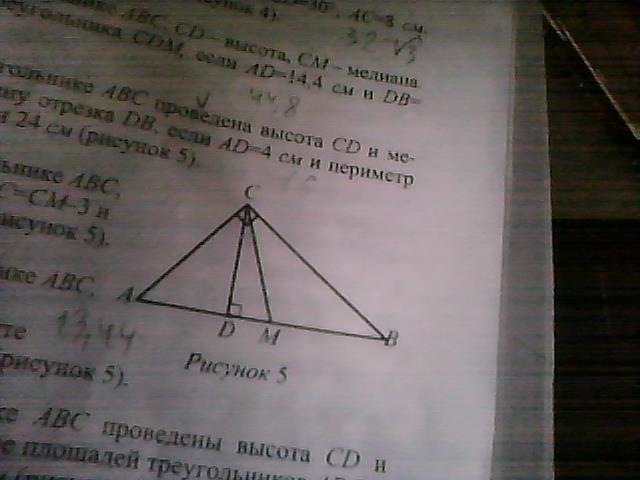
В прямоугольном треугольнике АВС,CD перпендикулярно AB, CM- медиана. CM=10 см и АС=12 см. Найдите периметр треугольника CDM

Answer 1

так как треугольник ABC прямоугольный треугольник и CM - медиана, то AM = MB = CM =10 см (если описать вокруг треугольника ABC окружность , то CM будет радиус, AB диаметр )
По теореме Пифагора найдем  CB
CB^2=AB^2-AC^2
CB^2=400-144=256
CB=16
Найдем DM:
CD^2=CB^2-DB^2
CD^2=CM^2-DM^2
CB^2-DB^2=CM^2-DM^2
256-DB^2=100-DM^2
DB^2-DM^2=156
(AM+DM)^2-DM^2=156
AM^2+2AM*DM+DM^2-DM^2=156
100 +20DM=156
DM=56/20=2,8 см
Найдем CD ( треугольник CDM прямоугольный CD⊥AB):
CD^2=CM^2-DM^2
CD^2=100-7,84=92,16
CD=9,6
P=9,6+10+2,8=22,4 см
Ответ 22,4 см