Question

Найти площадь фигуры ограниченной линиями

Answer 1

Найти площадь фигуры ограниченной линиями y=9-x²; y=0

Решение
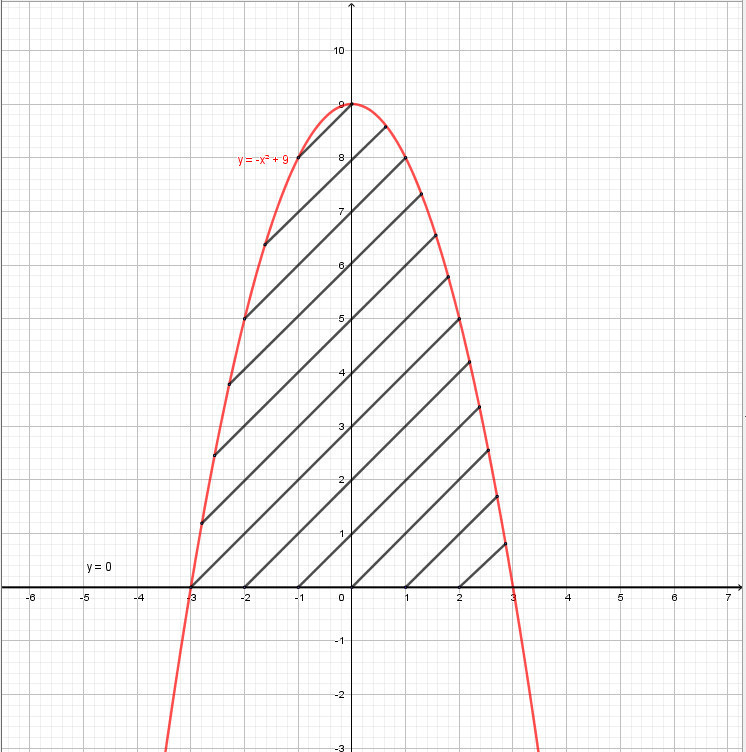
Графиком функции у = 9 - x² является парабола  ветви которой направлены вниз так как коэффициент перед х² меньше нуля.
Вершина параболы находится в точке х = 0, у = 9. 
Графиком функции у =0 является ось Oх.
Графики функции во вложении.
Найдем точки пересечения параболы и прямой решив систему уравнений
$left { {{y=0} atop {y=9-x^2}} right.$
Подставим первое уравнение во второе
                       9 - x² = 0
                            x² = 9
                     x₁ = -3                 x₂ = 3
 Нашли две точки пересечения заданных функций (-3;0) и (3;0).
Определим площадь отсеченной параболы найдя определенный интеграл
 $S = intlimits^3_{-3} {(9-x^2)} , dx=(9x - frac{x^3}{3}) left[begin{array}{ccc}3\-3end{array}right]=9*3- frac{3^3}{3}-9*(-3)+ frac{(-3)^3}{3}=$$27- 9+27-9=36$       

Ответ S = 36

Answer 2

Найти площадь фигуры ограниченной линиями y=-x²+9; y=0

Answer 3

В чем вопрос? Если в записи функции то 9 - x^2 = -x^2 + 9 (от перемены слагаемых сумма не меняется). На графике указана функция y = -x^2+9(по заданию). В тексте та же функция y = 9-x^2.