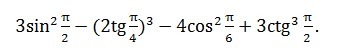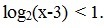Ответы
Ответ дал:
0
1) синус п/2=1, тангенс п/4=√2/2, косинус п/6=√3/2 ,котангес п/2=0
подставим 2*1-8*2√2/8-4√3/4+0=2-2√2-√3
2) из определения логарифма 2 в степени 1 больше х-3 поскольку два больше 1 х-3∠2
под логарифмом положительное число х-3>0
сводя оба решения получаем 0∠х∠5
3) х₁ =(10- √ ( 100-4*1*41)) /2 . х₁ = (10- √ - 64) /2 . х₁ = (10- 8i) /2 х₁=5- 4i
х₂= (10+√ ( 100-4*1*41)) /2 . х₂ = (10+ √ - 64) /2 . х₂ = (10+ 8i) /2 х₂=5+4i
4) ( -1+3i)/(1-2i) домножим числитель и знаменатель на 1+2i
( -1+3i)(1+2i)/(1-2i)(1+2i) (1-2i)(1+2i)=1-4i²=1+4=5
(-1-2i+3i-6)/5=(-7+i)/5
подставим 2*1-8*2√2/8-4√3/4+0=2-2√2-√3
2) из определения логарифма 2 в степени 1 больше х-3 поскольку два больше 1 х-3∠2
под логарифмом положительное число х-3>0
сводя оба решения получаем 0∠х∠5
3) х₁ =(10- √ ( 100-4*1*41)) /2 . х₁ = (10- √ - 64) /2 . х₁ = (10- 8i) /2 х₁=5- 4i
х₂= (10+√ ( 100-4*1*41)) /2 . х₂ = (10+ √ - 64) /2 . х₂ = (10+ 8i) /2 х₂=5+4i
4) ( -1+3i)/(1-2i) домножим числитель и знаменатель на 1+2i
( -1+3i)(1+2i)/(1-2i)(1+2i) (1-2i)(1+2i)=1-4i²=1+4=5
(-1-2i+3i-6)/5=(-7+i)/5
Вас заинтересует
3 года назад
3 года назад
9 лет назад
10 лет назад
10 лет назад