Question

Длины сторон треугольника относятся как m : n : k. Найти отношение площади этого треугольника к площади треугольника, вершины которого находятся в точках пересечения биссектрис со сторонами.

Answer 1

Биссектриса делит противоположную сторону пропорционально прилегающим сторонам
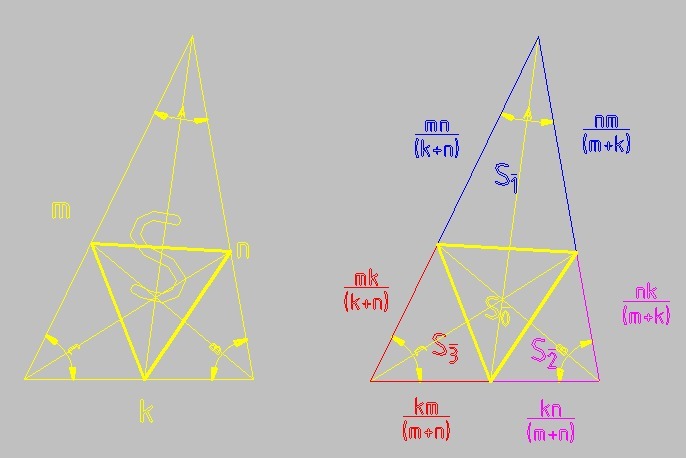
S - площадь исходного треугольника, S₁, S₂, S₃ - площади дочерних треугольников, прилегающие к вершинам, S₀ - площадь центрального дочернего треугольника
S₁ = 1/2*mn/(k+n)*nm/(m+k)*sin(A)
S =  1/2*mn*sin(A)
S₁ = S/(k+n)*1/(m+k)
Аналогично для других
S₂ = S/(m+k)*1/(m+n)
S₃ = S/(m+n)*1/(k+n)
---
S₀ = S(1- 1/(k+n)*1/(m+k) - 1/(m+k)*1/(m+n) - 1/(m+n)*1/(k+n))
S₀ = S(1- 2*(k+m+n)/((k+m)(k+n)(m+n))
Просят обратную величину.
Дроби там сокращаться не хотят вообще, поэтому просто перевернём
S/S₀ = 1/(1- 2*(k+m+n)/((k+m)(k+n)(m+n))