вершины треугольника делят описанную около него окружность на три дуги длины которых относятся как 6/7/23 найдите радиус окружности ечли меньшая из сторон треугольника равна 12
Ответы
Ответ дал:
0
6x +7x +23x =180° <=> x=180°/(6+7+23) =5°
В треугольнике против меньшей стороны лежит меньший угол.
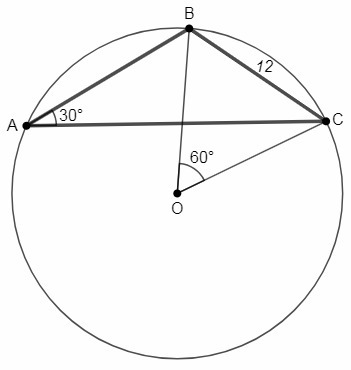
∠A= 6x =30°
По теореме синусов
BC/sinA =2R <=> R= 12/2sin30° =12
ИЛИ
Центральный угол вдвое больше вписанного угла, опирающегося на ту же дугу, ∠BOC=2∠BAC=60°. Равнобедренный треугольник (OB=ОС) с углом 60° - равносторонний, OB=BC=12
В треугольнике против меньшей стороны лежит меньший угол.
∠A= 6x =30°
По теореме синусов
BC/sinA =2R <=> R= 12/2sin30° =12
ИЛИ
Центральный угол вдвое больше вписанного угла, опирающегося на ту же дугу, ∠BOC=2∠BAC=60°. Равнобедренный треугольник (OB=ОС) с углом 60° - равносторонний, OB=BC=12
Приложения:
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад