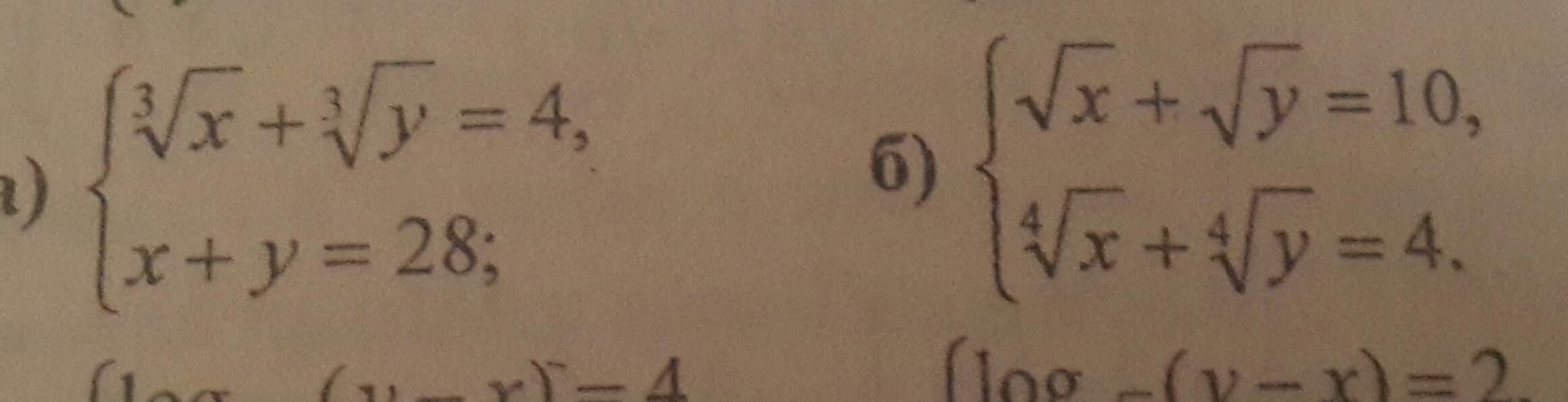Ответы
Ответ дал:
0
а)![left { {{ sqrt[3]{x}+ sqrt[3]{y} =4} atop {x+y=28}} right. left { {{ sqrt[3]{x}+ sqrt[3]{y} =4} atop {x+y=28}} right.](https://tex.z-dn.net/?f=+left+%7B+%7B%7B+sqrt%5B3%5D%7Bx%7D%2B+sqrt%5B3%5D%7By%7D++%3D4%7D+atop+%7Bx%2By%3D28%7D%7D+right.+)
![left { {{( sqrt[3]{x}+ sqrt[3]{y})^{3} =(4)^{3}} atop {x+y=28}} right. left { {{( sqrt[3]{x}+ sqrt[3]{y})^{3} =(4)^{3}} atop {x+y=28}} right.](https://tex.z-dn.net/?f=++left+%7B+%7B%7B%28+sqrt%5B3%5D%7Bx%7D%2B+sqrt%5B3%5D%7By%7D%29%5E%7B3%7D++%3D%284%29%5E%7B3%7D%7D+atop+%7Bx%2By%3D28%7D%7D+right.+)
![left { {{x+y+ 3sqrt[3]{x} sqrt[3]{y}(sqrt[3]{x}+ sqrt[3]{y} )=64} atop {x+y=28}} right. left { {{x+y+ 3sqrt[3]{x} sqrt[3]{y}(sqrt[3]{x}+ sqrt[3]{y} )=64} atop {x+y=28}} right.](https://tex.z-dn.net/?f=+left+%7B+%7B%7Bx%2By%2B+3sqrt%5B3%5D%7Bx%7D+sqrt%5B3%5D%7By%7D%28sqrt%5B3%5D%7Bx%7D%2B+sqrt%5B3%5D%7By%7D++%29%3D64%7D+atop+%7Bx%2By%3D28%7D%7D+right.+)
из за того, что x+y=28, а![sqrt[3]{x} + sqrt[3]{y}=4 sqrt[3]{x} + sqrt[3]{y}=4](https://tex.z-dn.net/?f=+sqrt%5B3%5D%7Bx%7D+%2B+sqrt%5B3%5D%7By%7D%3D4+) , тогда
, тогда
![left { {{28+ 3sqrt[3]{x} sqrt[3]{y}*4=64} atop {x+y=28}} right. left { {{28+ 3sqrt[3]{x} sqrt[3]{y}*4=64} atop {x+y=28}} right.](https://tex.z-dn.net/?f=+left+%7B+%7B%7B28%2B+3sqrt%5B3%5D%7Bx%7D+sqrt%5B3%5D%7By%7D%2A4%3D64%7D+atop+%7Bx%2By%3D28%7D%7D+right.+)
![left { {{12sqrt[3]{xy}=64-28} atop {x+y=28}} right. left { {{12sqrt[3]{xy}=64-28} atop {x+y=28}} right.](https://tex.z-dn.net/?f=+left+%7B+%7B%7B12sqrt%5B3%5D%7Bxy%7D%3D64-28%7D+atop+%7Bx%2By%3D28%7D%7D+right.+)
![left { {{sqrt[3]{xy}= frac{36}{12} } atop {x+y=28}} right. left { {{sqrt[3]{xy}= frac{36}{12} } atop {x+y=28}} right.](https://tex.z-dn.net/?f=+left+%7B+%7B%7Bsqrt%5B3%5D%7Bxy%7D%3D+frac%7B36%7D%7B12%7D+%7D+atop+%7Bx%2By%3D28%7D%7D+right.+)
![left { {{(sqrt[3]{xy})^{3}= 3^{3}} atop {x+y=28}} right. left { {{(sqrt[3]{xy})^{3}= 3^{3}} atop {x+y=28}} right.](https://tex.z-dn.net/?f=+left+%7B+%7B%7B%28sqrt%5B3%5D%7Bxy%7D%29%5E%7B3%7D%3D+3%5E%7B3%7D%7D+atop+%7Bx%2By%3D28%7D%7D+right.+)

(28-y)y=27
28y-y²=27
y²-28y+27=0
D=28²-4·1·27=784-108=676=26²
y₁=
y₂=
x₁=28-y₁=28-1=27
x₂=28-y₂=28-27=1
б)![(sqrt[4]{x})^{2} = a^{2} (sqrt[4]{x})^{2} = a^{2}](https://tex.z-dn.net/?f=+%28sqrt%5B4%5D%7Bx%7D%29%5E%7B2%7D+%3D+a%5E%7B2%7D)
![(sqrt[4]{y})^{2} = b^{2} (sqrt[4]{y})^{2} = b^{2}](https://tex.z-dn.net/?f=+%28sqrt%5B4%5D%7By%7D%29%5E%7B2%7D+%3D+b%5E%7B2%7D)




(4-b)²+b²=10
16-8b+b²+b²-10=0
2b²-8b+6=0 (:2)
b²-4b+3=0
D=16-12=4=2²
b₁=
b₂=
a₁=4-1=3
a₂=4-3=1

x=a⁴

y=b⁴
x₁=a₁⁴=3⁴=81
y₁=b₁⁴=1⁴=1
x₂=a₂⁴=1⁴=1
y₂=b₂⁴=3⁴=81
из за того, что x+y=28, а
(28-y)y=27
28y-y²=27
y²-28y+27=0
D=28²-4·1·27=784-108=676=26²
y₁=
y₂=
x₁=28-y₁=28-1=27
x₂=28-y₂=28-27=1
б)
(4-b)²+b²=10
16-8b+b²+b²-10=0
2b²-8b+6=0 (:2)
b²-4b+3=0
D=16-12=4=2²
b₁=
b₂=
a₁=4-1=3
a₂=4-3=1
x=a⁴
y=b⁴
x₁=a₁⁴=3⁴=81
y₁=b₁⁴=1⁴=1
x₂=a₂⁴=1⁴=1
y₂=b₂⁴=3⁴=81
Вас заинтересует
3 года назад
3 года назад
9 лет назад