Question

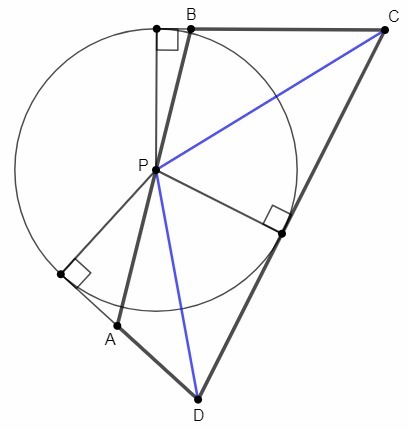
в выпуклом четырехугольнике abcd биссектрисы углов c и b пересекаются на стороне ab в точке p докажите , что точка p равноудалена от сторон четырехугольника.
Задача из второй части ОГЭ, точно не помню была ли дана сторона, но в голове крутится, что равна 9 или 12(аб). Ну,даже если бы сторона не была дана, как ее можно решить?

Answer 1

Биссектриса угла - геометрическое место точек, равноудаленных от сторон угла. Точка P лежит на биссектрисе угла BCD, следовательно равноудалена от сторон BC, CD. Точка P лежит на биссектрисе угла CDA, следовательно равноудалена от сторон CD, AD. Таким образом, точка P равноудалена от трех сторон: BC, CD, AD.