Question

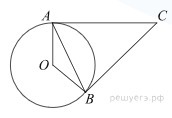
Касательные в точ­ках A и B к окруж­но­сти с цен­тром O пе­ре­се­ка­ют­ся под углом 18°. Най­ди­те угол AOB. Ответ дайте в градусах.

Answer 1

<АО = 360°-90°-90°-18°=162°
Ответ:162°

Answer 2

180-18=162

Answer 3

?????

Answer 4

∠ACB=18°  
так как касательные ⊥ радиусам в точке касания то ∠OAC=∠OBC=90°
треугольники ОАС и ОВС прямоугольные у них 
катеты ОА=ОВ так как это радиусы и гипотенуза ОС общая
⇒ОАС=ОВС по катету и гипотенузе
⇒∠АСО=∠ВСО=18°/2=9°
∠AOC=∠BOC=90°-9°=81°
∠AOB=∠AOC+∠BOC=81+81=162°