Ребята, помогите пожалуйста! Не могу понять, как решается задачка. Если не трудно - объясните пожалуйста.
Найти все действительные значения b, при которых X1 и X2 уравнения x^2+bx+4b=0 действительные и такие, что x1>-1 и x2>-1
Ответы
Ответ дал:
0
Решение задания приложено
Приложения:
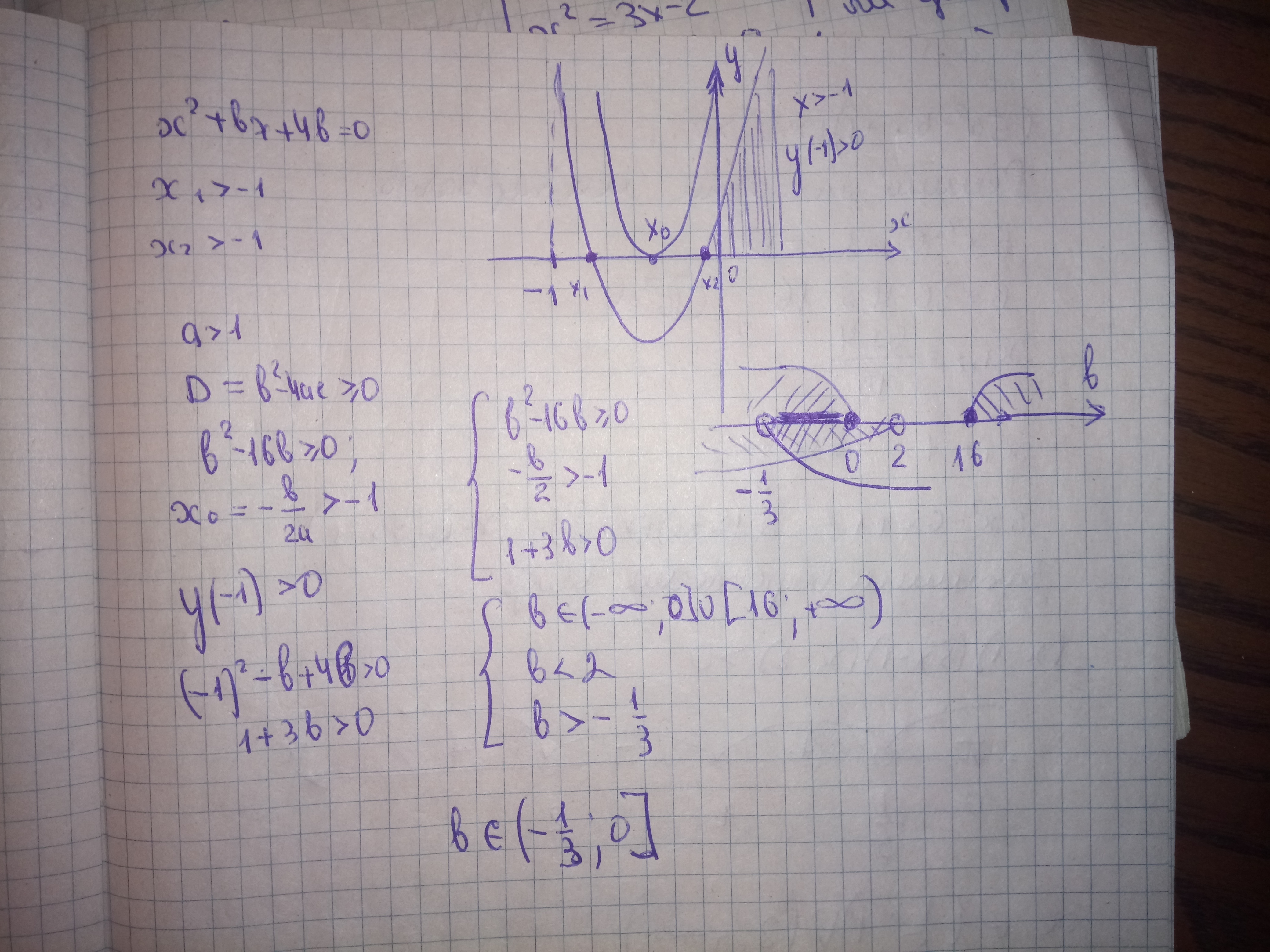
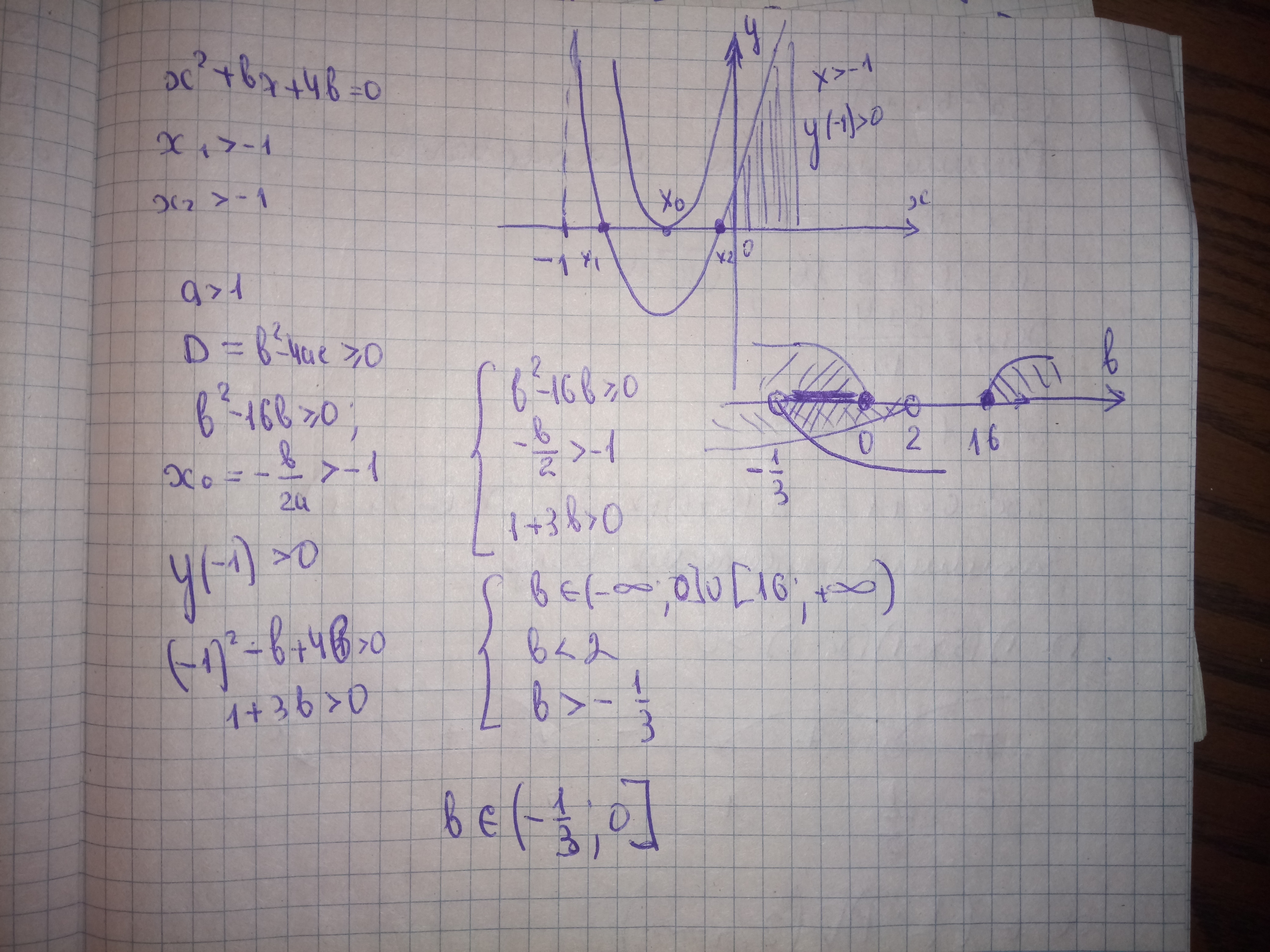
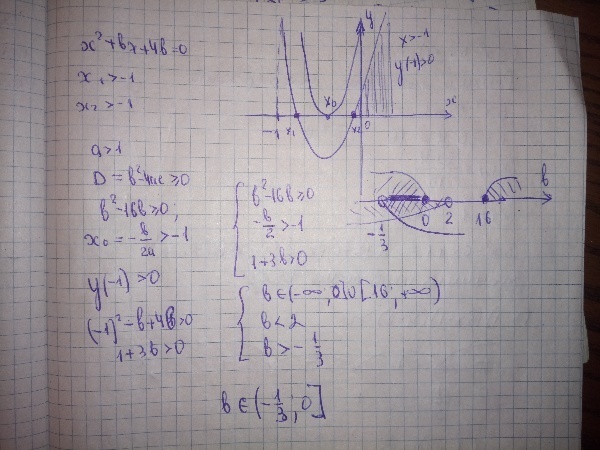
Ответ дал:
0
На мой взгляд, решение неверное. Достаточно взять в = - 1/4, показать, что для данного значения b выполнены все условия:
1) x^2 - 1/4x - 1 = 0, D > 0, оба корня - действительные числа.
2) Каждый корень больше - 1.
Если я права, то исправьте, пожалуйста, решение.
1) x^2 - 1/4x - 1 = 0, D > 0, оба корня - действительные числа.
2) Каждый корень больше - 1.
Если я права, то исправьте, пожалуйста, решение.
Ответ дал:
0
Приведу и второе доказательство ошибочности решения:
Если b = 20, то уравнение x^2+20x+80=0 имеет два корня, меньшие - 5, что не удовлетворяет условию задачи.
Если b = 20, то уравнение x^2+20x+80=0 имеет два корня, меньшие - 5, что не удовлетворяет условию задачи.
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад