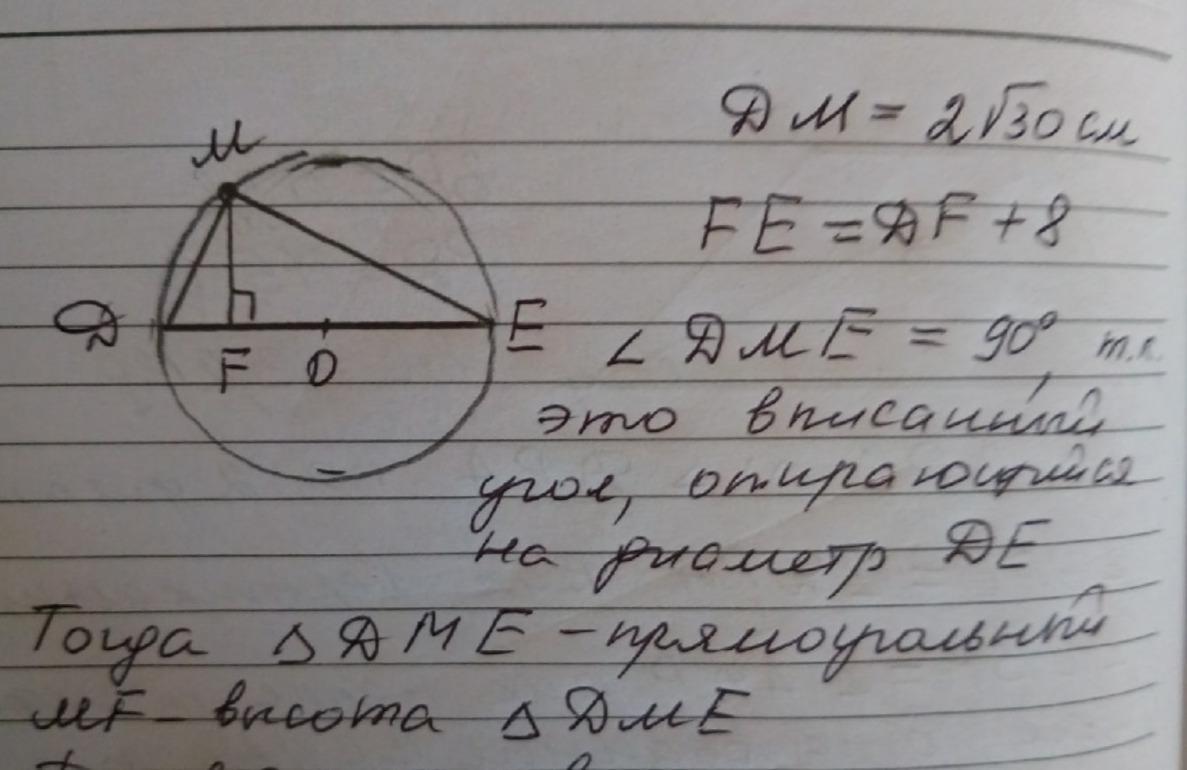
Из точки M окружности опущен перпендикуляр MF на ее диаметр DE,
DM=2√30 см . Найдите радиус окружности, если отрезок DF на 8 см меньше отрезка FE
Ответы
x+x+8=2R
R=(2x+8)/2=x+4
MF^2=DM^2-DF^2=(2√30)^2-x^2=120-x^2
MF^2=ME^2-FE^2=DE^2-MD^2-FE^2=(2x+8)^2-(2√30)^2-(x+8)^2=4x^2+32x+64-120-x^2-16x-64=3x^2+16x-120
120-x^2=3x^2+16x-120
4x^2+16x-240=0
D=16^2-4*4*(-240)=4096
x1=(-16+√4096)/2*4=6
x2=(-16-√4096)/2*4=-10
=>x=6
R=6+4=10
Ответ:
Радиус окружности = 10 см.
Объяснение:
Рисунок в приложении. Центр окружности - т.O.
Пусть отрезок DF = x см. Тогда отрезок FE = x + 8 см, а диаметр DE = DF + FE = x + x + 8 = 2x + 8 см.
Радиус окружности равен половине диаметра, R = (2x + 8)/2 = x + 4.
⇒FO = R - x = x + 4 - x = 4.
Проведем радиус MO.
ΔMFO прямоугольный, ∠F = 90°. В ΔMFO выразим MF² через x по т.Пифагора.
MF² = MO² - FO² = (x + 4)² - 16 = x² + 8x +16 - 16 = x² + 8x.
ΔDMF прямоугольный, ∠F = 90°. По т.Пифагора:
DM² = DF² + MF²;
(2√30)² = x² + x² + 8x;
4*30 = 2x² + 8x; (разделим обе части уравнения на 2);
x² + 4x - 60 = 0;
D = b² - 4ac = 16 + 240 = 256 = 16²;
x₁ = (-b - √D)/2a = (-4 - 16)/2 = - 10 (не является решением задачи);
x₂ = (-b + √D)/2a = (-4 + 16)/2 = 6;
DF = 6 см, радиус R = 6 + 4 = 10 см.

Ответ:
решение представлено на фото
Объяснение: