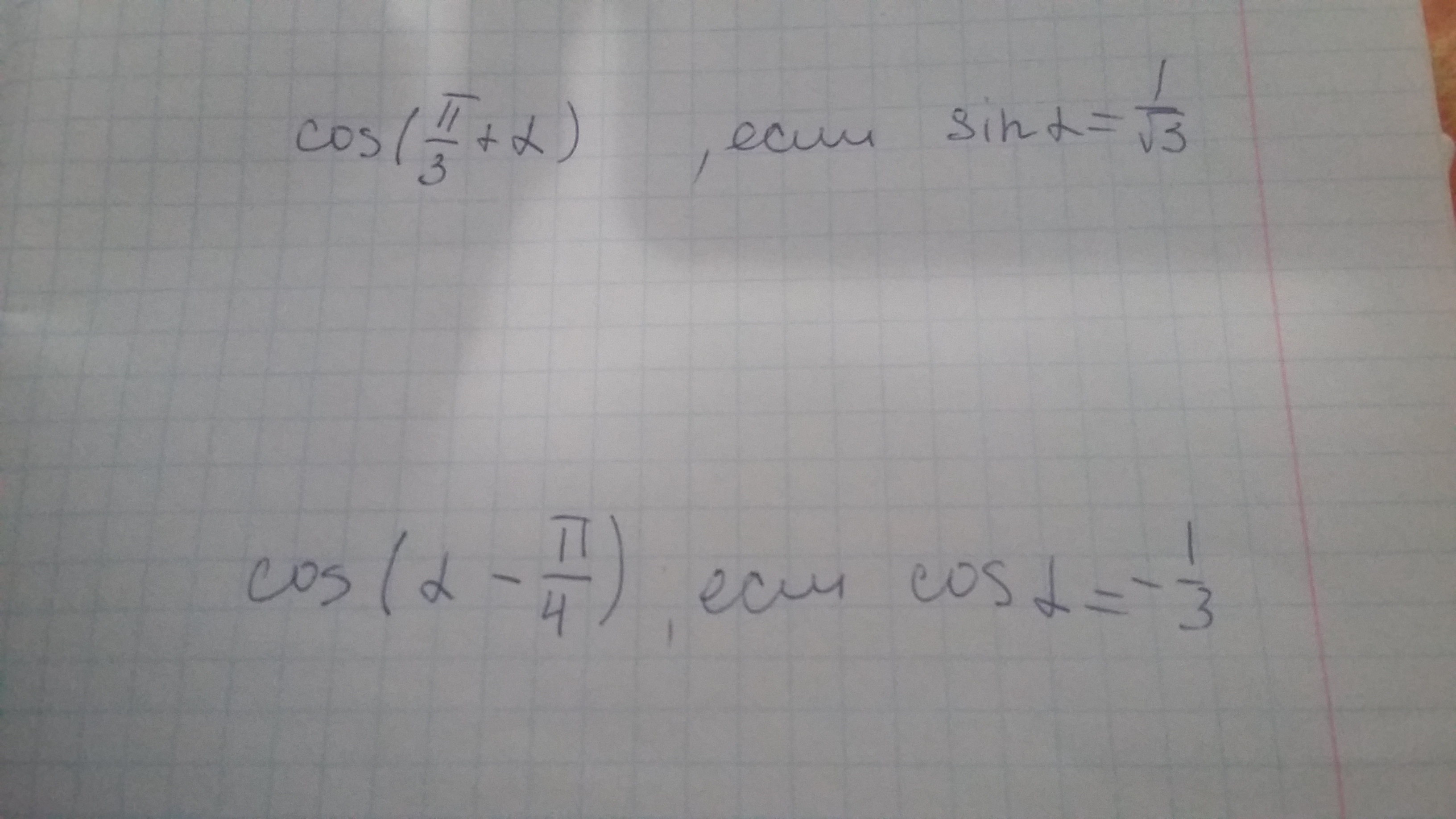Ответы
Ответ дал:
0
1.
а) По формуле косинус суммы получаем:

б) Воспользуемся основным тригонометрическим тождеством:

α находится в промежутке от 0 до π/2 (1-ая четверть). Из этого следует, что значение косинуса на этом промежутке будет положительным.
в) Подставляем вместо синуса и косинуса соответствующие им значения:

2.
а) По формуле косинус разности получаем:

б) Аналогично первой задаче находим значение синуса, а так как π/2<α<π, синус будет отрицательным.

в)

а) По формуле косинус суммы получаем:
б) Воспользуемся основным тригонометрическим тождеством:
α находится в промежутке от 0 до π/2 (1-ая четверть). Из этого следует, что значение косинуса на этом промежутке будет положительным.
в) Подставляем вместо синуса и косинуса соответствующие им значения:
2.
а) По формуле косинус разности получаем:
б) Аналогично первой задаче находим значение синуса, а так как π/2<α<π, синус будет отрицательным.
в)
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад