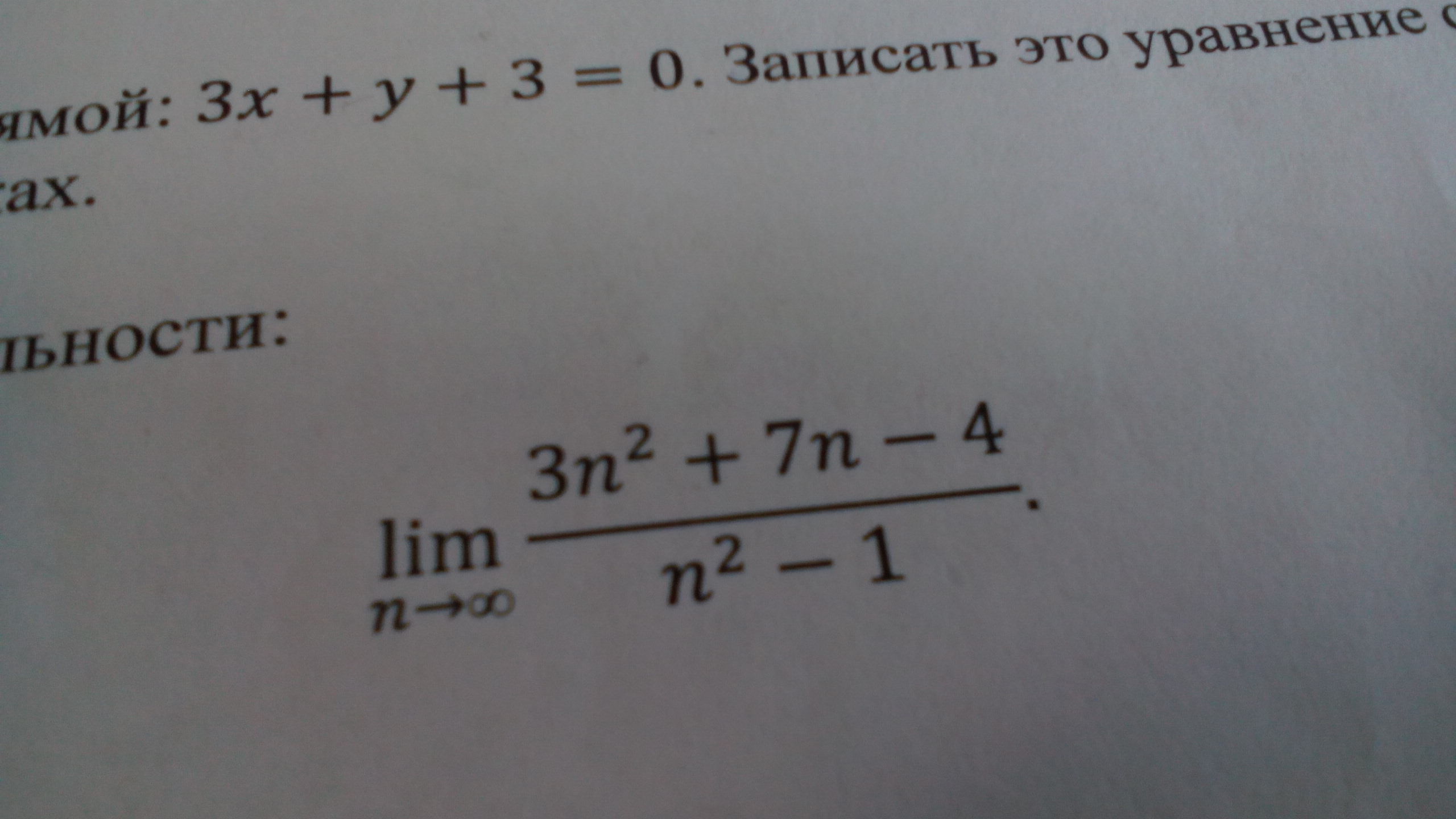Ответы
Ответ дал:
0
lim(n→∞) (3n²+7n-4)/(n²-1)
Разделим одновременно числитель и знаменатель на n²:
lim(n→∞) (3n²/n²+7n/n²-4/n²)/(n²/n²-1/n²)=lim(n→∞) (3+7/n-4/n²)/(1-1/n²)=
=(3+0-0)/(1-0)=3/1=3.
Ответ: lim(n→∞) (3n²+7n-4)/(n²-1)=3.
Разделим одновременно числитель и знаменатель на n²:
lim(n→∞) (3n²/n²+7n/n²-4/n²)/(n²/n²-1/n²)=lim(n→∞) (3+7/n-4/n²)/(1-1/n²)=
=(3+0-0)/(1-0)=3/1=3.
Ответ: lim(n→∞) (3n²+7n-4)/(n²-1)=3.
Вас заинтересует
2 года назад
9 лет назад
9 лет назад
10 лет назад