Question

(x+2)(5x+3)-5(x+2)(x-2)⩽10 найдите множество решений неравенства

Answer 1

(x+2)(5x+3)-5(x+2)(x-2)⩽10  

5х²+10х+3х+6-5х²+20≤10  
13х≤-16  
х≤-16/13  
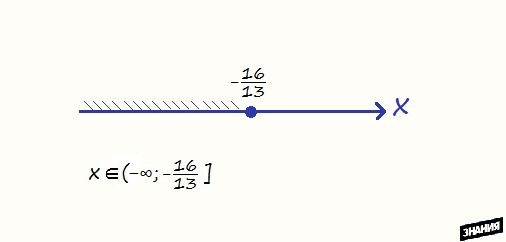
х∈(-∞;-16/13]

Answer 2

РЕШЕНИЕ:

$bold{(x+2)(5x+3)-5(x+2)(x-2) leq 10} \ \ 5x^2+3x+10x+6 - 5x^2+20 leq 10 \ \ 13x+6+20 leq 10 \ \ 13x + 26 leq 10 \ \ 13x leq 10-26 \ \ 13x leq -16 \ \ x leq - dfrac{16}{13} \ \ \ x in (- infty; -frac{16}{13}]$

В ответ записываем промежуток. 

ОТВЕТ: (-∞; $- frac{16}{13}$]