Помогите пожалуйста)))
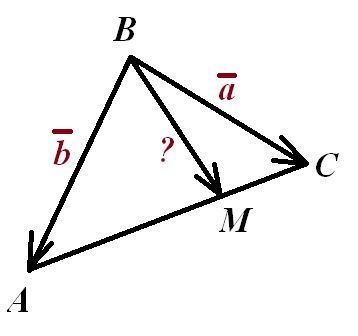
В треугольнике ABC сторона AC разделена точкой M в отношении 3:1, считая от точки A. Какой вид имеет разложение вектора BM по векторам a=BC и b=BA?
Ответы
Ответ дал:
0
По правилу треугольника в ΔАВС: 
Значит,
По условию АМ:МС=3:1, тогда

По правилу треугольника в ΔВМС:

Ответ:
Значит,
По условию АМ:МС=3:1, тогда
По правилу треугольника в ΔВМС:
Ответ:
Приложения:
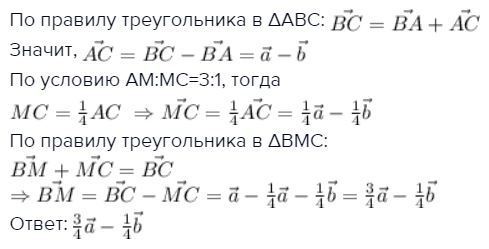
Вас заинтересует
2 года назад
3 года назад
9 лет назад
10 лет назад
10 лет назад