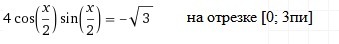Ответы
Ответ дал:
0
4sin(x/2)cos(x/2)=-√3
2sin(2*x/2)=2sinx
2sinx=-√3
sinx=-√3/2
x1=4pi/3+2pik и x2=5pi/3+2pik
На данном интервале два корня
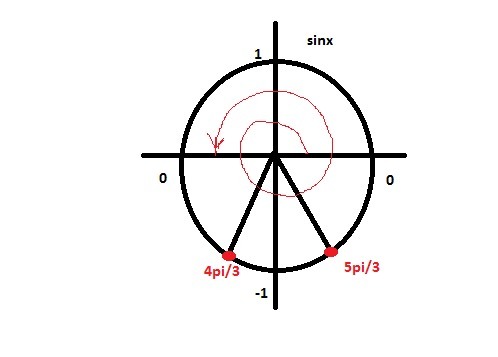
x={4pi/3;5pi/3}
2sin(2*x/2)=2sinx
2sinx=-√3
sinx=-√3/2
x1=4pi/3+2pik и x2=5pi/3+2pik
На данном интервале два корня
x={4pi/3;5pi/3}
Приложения:
Ответ дал:
0
это каким то образом находят , но я не понимаю как!
Ответ дал:
0
есть формулы приведения по всем основным тригонометрическим функциям...
Ответ дал:
0
Ты не можешь объяснить???
Ответ дал:
0
нет, я уже все написала
Ответ дал:
0
ты норм???сама не знаешь как решать , а корни я и сама знаю, мне нужно знать как и получить!
Ответ дал:
0
2 корней
показание
решите с помощью единичний окружности
4cos(x/2)sin(x/2)=-√3
2sin(2*x/2)=-√3
sinx=-√3/2
показание
решите с помощью единичний окружности
4cos(x/2)sin(x/2)=-√3
2sin(2*x/2)=-√3
sinx=-√3/2
Приложения:
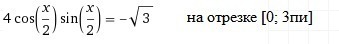
Ответ дал:
0
sinx=-√3/2 - вот это я понимаю , а как дальше понять что два корня ???
Ответ дал:
0
1) sin(-pi/3)=--√3/2 sinsin(4pi/3)=-√3/2
Ответ дал:
0
Извините 1) sin(-pi/3)=--√3/2 sinsin(4pi/3)=-√3/2
Ответ дал:
0
Извините. 1) sin(-pi/3)=--√3/2 sin(-pi/3+2pi)=sin(5pi/3)=-√3/2 2)sin(4pi/3)=-√3/2 Ответ: 4пи/3; 5пи/3
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад