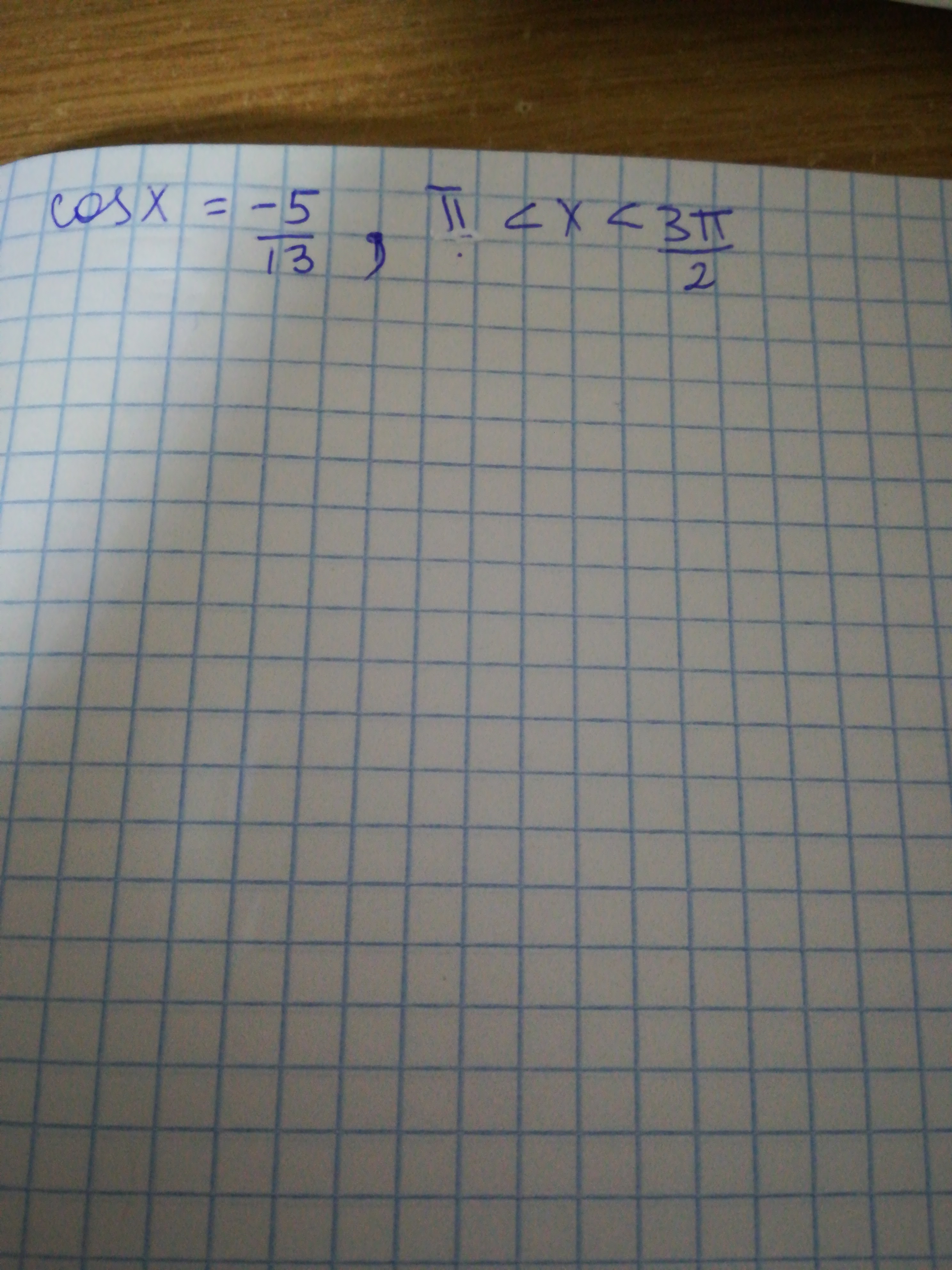Ответы
Ответ дал:
0
Формула: cos^2a + sin^2a = 1 => 1-cos^2a (для sin a)
Получается:
cosx=-5/13
sin^2a = 1 - (-5/13)^2 = 1 - 25/169 (169/169 - 25/169)
sin^2a = 144/169
sin a = √144/169 = 12/13
sin a = +- 12/13, а так как π < x < 3π/2 => Значит, отрицательный знак
Ответ: sin a = -12/13
Получается:
cosx=-5/13
sin^2a = 1 - (-5/13)^2 = 1 - 25/169 (169/169 - 25/169)
sin^2a = 144/169
sin a = √144/169 = 12/13
sin a = +- 12/13, а так как π < x < 3π/2 => Значит, отрицательный знак
Ответ: sin a = -12/13
Ответ дал:
0
Основное тригонометрическое тождество: sin²x + cos²x = 1 ⇒ sin²x = 1 - cos²x.
В данном случае: sin²x = , т.е. sin²x =
, т.е. sin²x =  .
.
Функция y = sinx может принимать как неотрицательные, так и отрицательные значения. Посмотрим на ограничение на x: он лежит в третьей четверти, где sinx отрицательный (sin - это ось, совпадающая с осью y, как видим, значения там отрицательные). Значит, sinx = .
.
Ответ: .
.
Задавайте вопросы в комментариях, если что-то непонятно.
В данном случае: sin²x =
Функция y = sinx может принимать как неотрицательные, так и отрицательные значения. Посмотрим на ограничение на x: он лежит в третьей четверти, где sinx отрицательный (sin - это ось, совпадающая с осью y, как видим, значения там отрицательные). Значит, sinx =
Ответ:
Задавайте вопросы в комментариях, если что-то непонятно.
Вас заинтересует
2 года назад
2 года назад
3 года назад
10 лет назад
10 лет назад