Нужно найти производную f(x)= .Мнения расходяться: одни считают что его нужно логарифмировать(y=(sin(x)*ln(x))',другие просто считают как сложную функцию(sin(x)*x^(sin(x)-1)*cos(x)),другие по формуле,как все-таки правильно?
.Мнения расходяться: одни считают что его нужно логарифмировать(y=(sin(x)*ln(x))',другие просто считают как сложную функцию(sin(x)*x^(sin(x)-1)*cos(x)),другие по формуле,как все-таки правильно?
Ответы
Ответ дал:
0
Удобнее свести к экспоненциальной функций, именно
y=x^sinx = e^(ln(x^sinx))
И как сложную функцию
y’=e^(ln(x^sinx))*(ln(x^sinx))’=
x^sinx * (lnx*sinx)’ = x^sinx * (sin(x)/x + lnx*cosx) = x^(sinx-1) * (sinx + x*lnx*cosx)
y=x^sinx = e^(ln(x^sinx))
И как сложную функцию
y’=e^(ln(x^sinx))*(ln(x^sinx))’=
x^sinx * (lnx*sinx)’ = x^sinx * (sin(x)/x + lnx*cosx) = x^(sinx-1) * (sinx + x*lnx*cosx)
Ответ дал:
0
Это производная сложной функции.
Приложения:
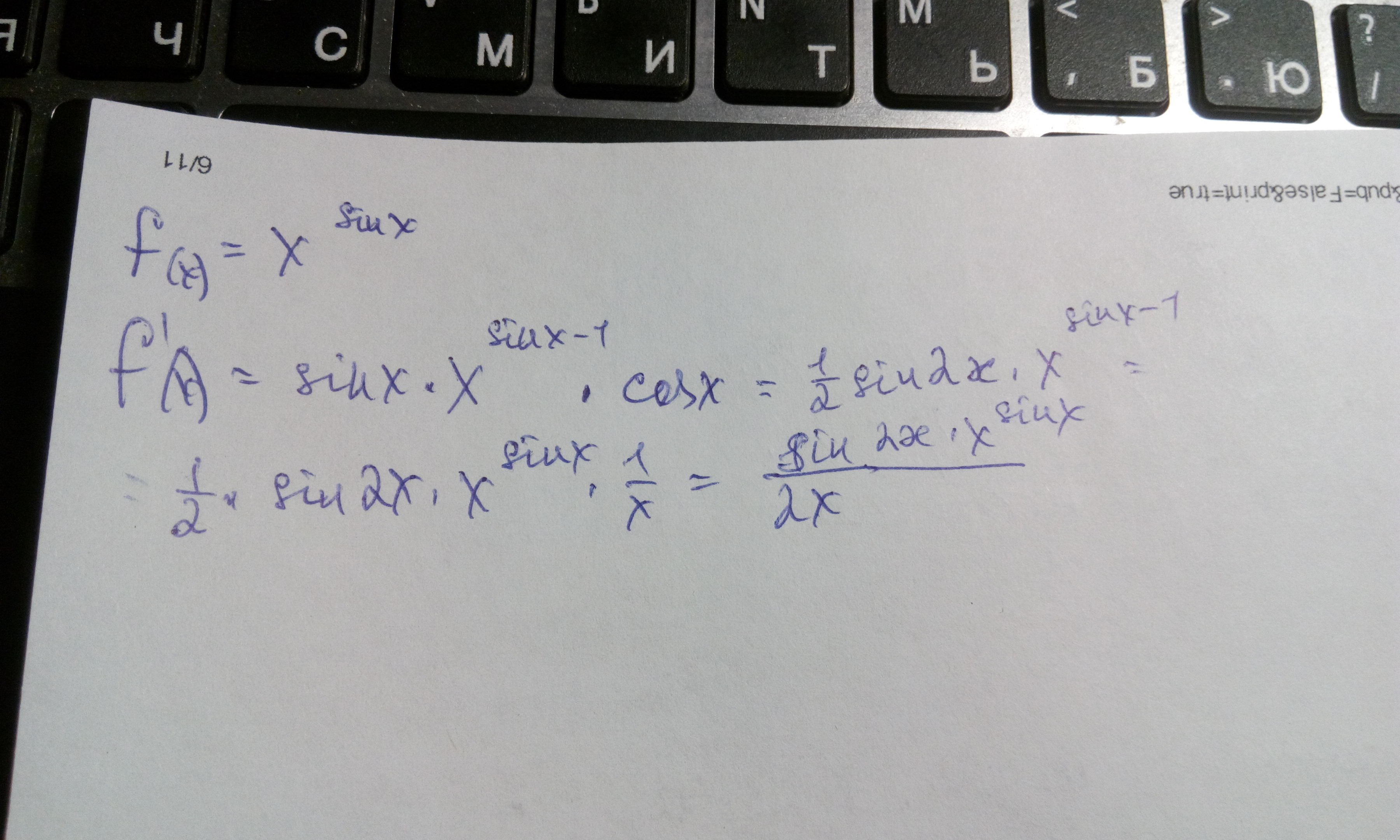
Ответ дал:
0
настоящий подчерк
Ответ дал:
0
ни одной подписки и 456 подписчиков
Ответ дал:
0
даааа
Ответ дал:
0
клёво
Ответ дал:
0
Нет , здесь же Sinx это тоже переменная , это не константа
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад