Ответы
Ответ дал:
0
Найдём пределы интегрирования:
x^2+4x=x+4
x^2+3x-4=0
D= 9+16=25
x1= (-3-5)/2= -4
x2= (-3+5)/2= 1
x^2+4x=x+4
x^2+3x-4=0
D= 9+16=25
x1= (-3-5)/2= -4
x2= (-3+5)/2= 1
Приложения:
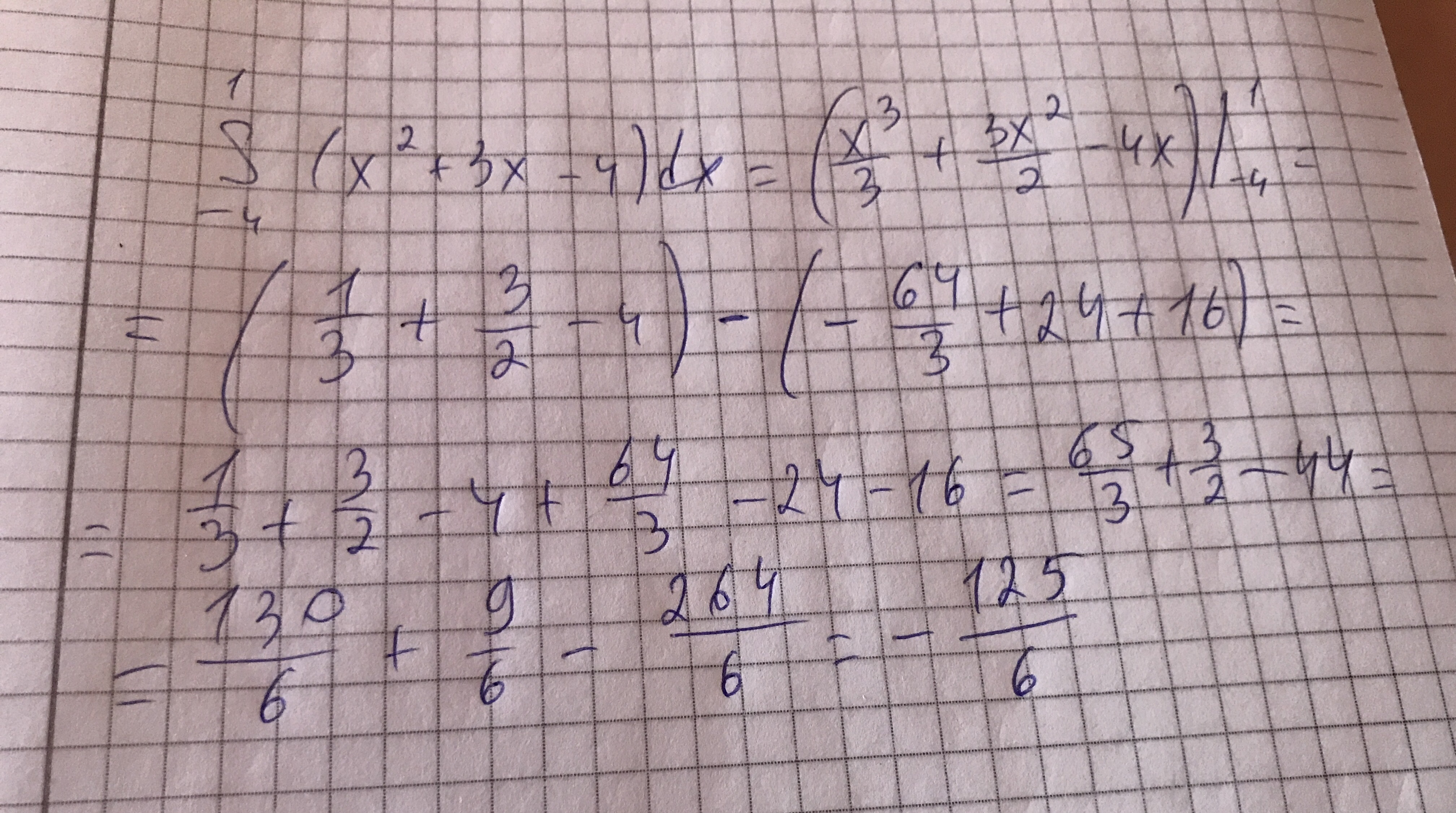
Ответ дал:
0
Если не ошибаюсь, ответ должен быть положительным числом
Ответ дал:
0
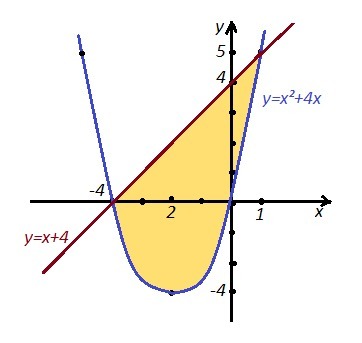
Точки пересечения:  .
.

Приложения:
Ответ дал:
0
Спасибо!
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад