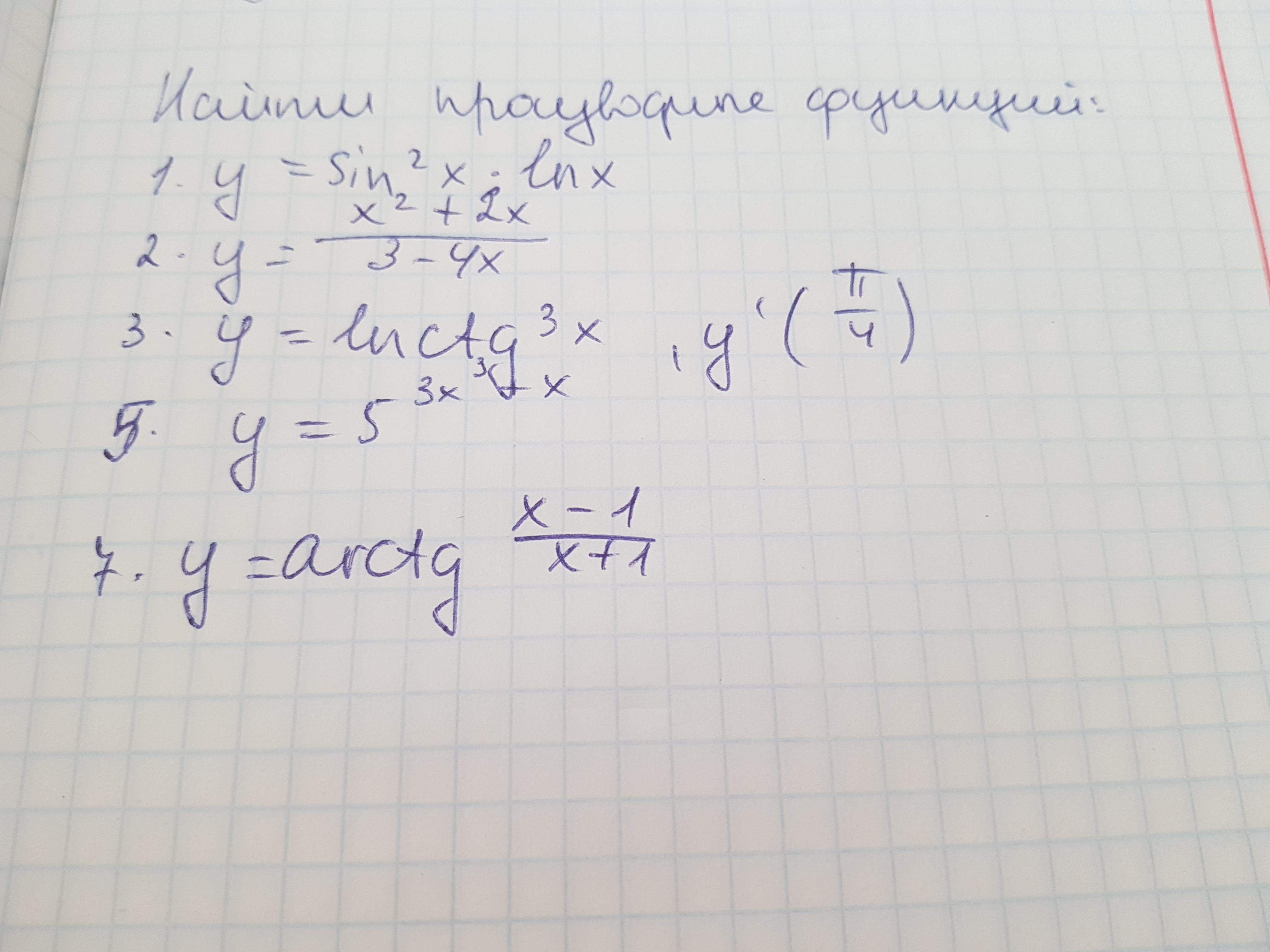Ответы
Ответ дал:
0
Ответ дал:
0
1. 
2.
3.

5.
7.
все решается просто подставляя в формулы
2.
3.
5.
7.
все решается просто подставляя в формулы
Приложения:
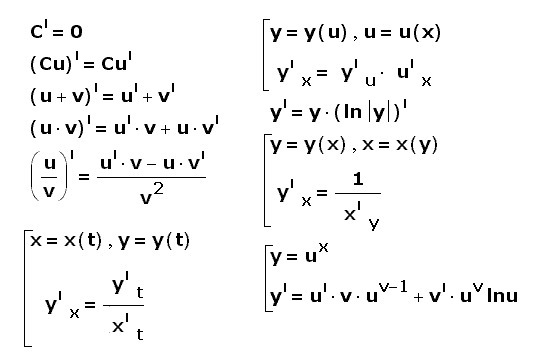
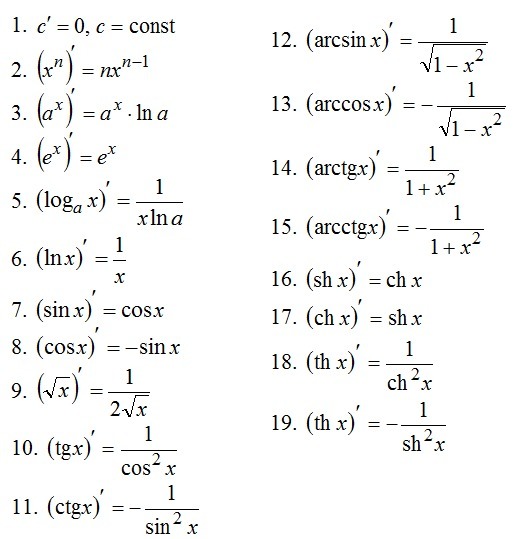
Ответ дал:
0
нет, вы хотите получить баллы, вот и будьте добры за них расписать все
Ответ дал:
0
каждый сам решает на сколько ему расписать свое решение. воля автора выбрать лучшее решение
Ответ дал:
0
нет, прочтите правила сервиса, решение должно быть полное, должны быть даны ответы на все пункты
Ответ дал:
0
окей, согласен, не прав
Ответ дал:
0
ща дополним
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад