Помогите пожалуйста...
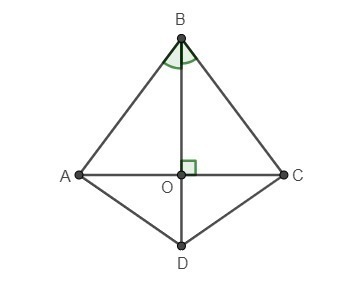
В четырехугольнике диагонали АС и BD перпендикулярны. Диагональ BD образует со сторонами BA и BC равные углы. Доказать, что AD=DC.
Ответы
Ответ дал:
0
Рассмотрим прямоугольные треугольники АВО и СВО:
∠АВО = ∠СВО по условию
ВО - общий катет
Следовательно, ΔАВО = ΔСВО по катету и прилежащему острому углу.
В равных треугольниках соответствующие элементы равны, отсюда:
АО = СО
Рассмотрим треугольник АDС:
DО ⊥ АС (по условию) ⇒ DО - высота
АО = СО (доказано выше) ⇒ DО - медиана
Если DО является медианой и высотой, тогда ΔАDС - равнобедренный, с основанием АС, отсюда:
АD = DС, что и требовалось доказать.
∠АВО = ∠СВО по условию
ВО - общий катет
Следовательно, ΔАВО = ΔСВО по катету и прилежащему острому углу.
В равных треугольниках соответствующие элементы равны, отсюда:
АО = СО
Рассмотрим треугольник АDС:
DО ⊥ АС (по условию) ⇒ DО - высота
АО = СО (доказано выше) ⇒ DО - медиана
Если DО является медианой и высотой, тогда ΔАDС - равнобедренный, с основанием АС, отсюда:
АD = DС, что и требовалось доказать.
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад