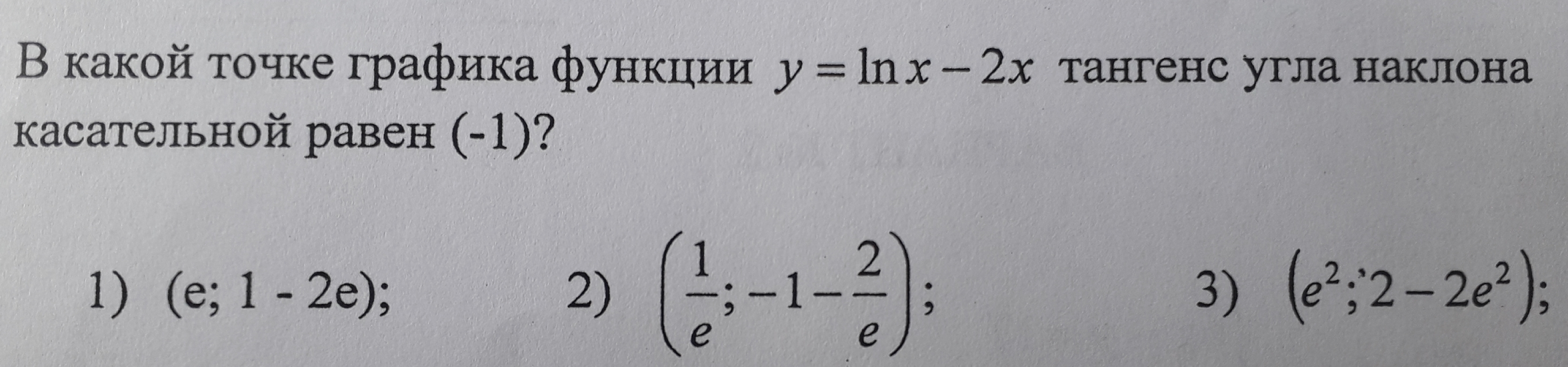Ответы
Ответ дал:
0
геометрический смысл производной:
производная функции, вычисленная в точке касания равна угловому коэффициенту касательной или тангенсу угла наклона
f'(x₀)=k=tgα
x₀ - абсцисса точки касания
α - угол между касательной к графику функции и положительным направлением оси Ох
tgα = - 1, => f'(x₀) = -1
f'(x)=(lnx-2x)'= 1/x-2

 , =>
, =>
x₀=1
f(x₀)=f(1)=ln1-2*1=0-2=-2
координаты точки касания:
(1;-2)
производная функции, вычисленная в точке касания равна угловому коэффициенту касательной или тангенсу угла наклона
f'(x₀)=k=tgα
x₀ - абсцисса точки касания
α - угол между касательной к графику функции и положительным направлением оси Ох
tgα = - 1, => f'(x₀) = -1
f'(x)=(lnx-2x)'= 1/x-2
x₀=1
f(x₀)=f(1)=ln1-2*1=0-2=-2
координаты точки касания:
(1;-2)
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад