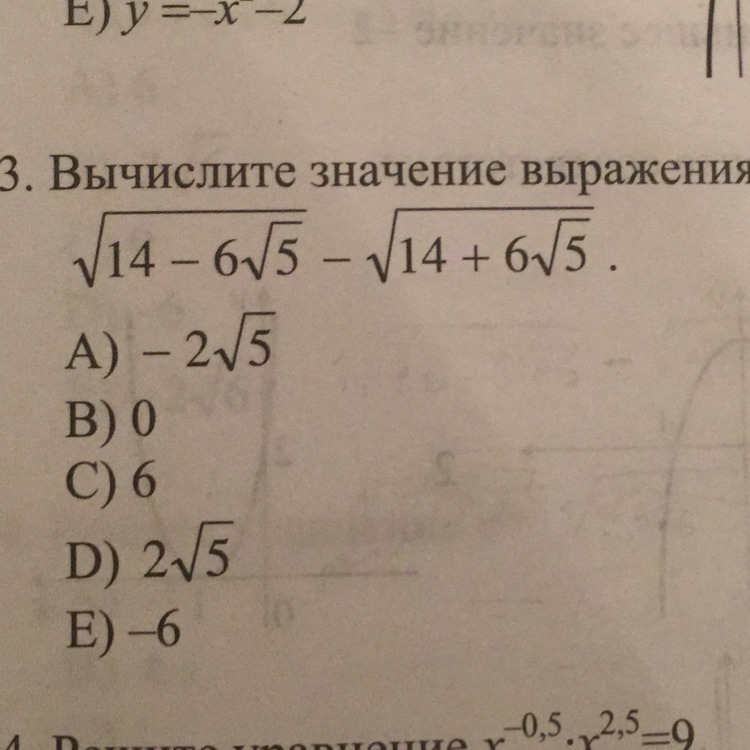Question

Помогите с решением плз!!!!!!!!

Answer 1

√(14-6√5)-√(14+6√5)=√(9-6√5+5)-√(9+6√5+5)=√(3²-2·3·√5+(√5)²)-√(3²+2·3·√5+(√5)²)=√(3-√5)²-√(3+√5)²=3-√5-3+√5=-2√5

Answer 2

между корнями в условии стоит минус, а у вас плюс.

Answer 3

исправьте...

Answer 4

√(14+6√5)-√(14-6√5)=√(9+6√5+5)+√(9-6√5+5)=
√(3²+2·3·√5+(√5)²)-√(3²-2·3·√5+(√5)²=√(3+√5)²-√(3-√5)²=
3+√5-3-√5=0

Answer 5

исправить надо в вашем тексте ответа . И исправить правильно. То, что вы написали, неверно

Answer 6

условие теперь неверно нписали...

Answer 7

$14-6sqrt5=(a-b)^2=a^2-2ab+b^2; ;\\14-6sqrt5=14-2cdot underbrace {3}_{a}cdot underbrace {sqrt5}_{b}=underbrace {9}_{a^2}+underbrace {5}_{b^2}-2cdot 3cdot sqrt5=\\=(3-sqrt5)^2; ;\\\14+6sqrt5=(3+sqrt5)^2; ;\\\sqrt{14-6sqrt5}-sqrt{14+6sqrt5}=sqrt{(3-sqrt5)^2}-sqrt{(3+sqrt5)^2}=\\=|underbrace {3-sqrt5}_{ textgreater 0}|-|underbrace{3+sqrt5}_{ textgreater 0}|=3-sqrt5-(3+sqrt5)=-2sqrt5$

При раскрытии модулей учтём, что модуль положительного выражения равен самому этому выражению.