Question

Боковое ребро прямой четырёхугольной призмы равно 4, основанием призмы является прямоугольник с диагональю 6 см и одной из сторон 4 см. Найдите площадь полной поверхности призмы

Answer 1

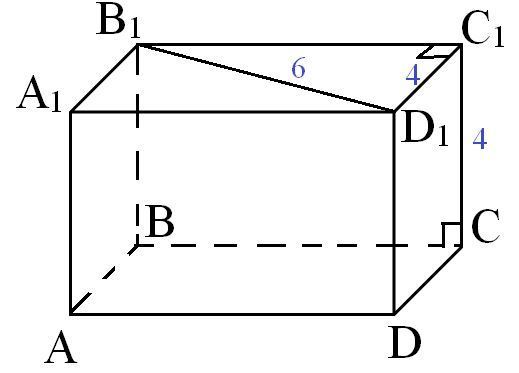
Визуализация - во вложении.
Пусть ABCDA1B1C1D1 - данная призма. Т.к. в её основании прямоугольник, и по условию призма прямая, то ABCDA1B1C1D1 - прямоугольный параллелепипед.
Для прямоугольного параллелепипеда, измерения которого - a, b и с, площадь волной поверхности ищем по формуле S=2(ab+ac+bc).
Рассмотрим прямоугольный Δ В1D1C1. По теореме Пифагора
$B_1C_1= sqrt{6^2-4^2} = sqrt{20} = 2sqrt{5}$ см.
$S=2(ab+ac+bc) = 2(4*4+4*2 sqrt{5} +4*2 sqrt{5} )=32+32 sqrt{5}$ см².
Ответ: 32(1+$sqrt{5}$) см²