Ответы
Ответ дал:
0
решила некоторые!!!!!!!!!
Приложения:



Ответ дал:
0
● Нр.1
![sqrt[5]{243 {m}^{5} } + sqrt[4]{16 {m}^{4} } - sqrt{36 {m}^{2} } = sqrt[5]{ {3}^{5} {m}^{5} } + sqrt[4]{ {2}^{4} {m}^{4} } - sqrt{ {6}^{2} {m}^{2} } = 3m + 2m - 6m = - m sqrt[5]{243 {m}^{5} } + sqrt[4]{16 {m}^{4} } - sqrt{36 {m}^{2} } = sqrt[5]{ {3}^{5} {m}^{5} } + sqrt[4]{ {2}^{4} {m}^{4} } - sqrt{ {6}^{2} {m}^{2} } = 3m + 2m - 6m = - m](https://tex.z-dn.net/?f=+sqrt%5B5%5D%7B243+%7Bm%7D%5E%7B5%7D+%7D+%2B+sqrt%5B4%5D%7B16+%7Bm%7D%5E%7B4%7D+%7D+-+sqrt%7B36+%7Bm%7D%5E%7B2%7D+%7D+%3D+sqrt%5B5%5D%7B+%7B3%7D%5E%7B5%7D+%7Bm%7D%5E%7B5%7D+%7D+%2B+sqrt%5B4%5D%7B+%7B2%7D%5E%7B4%7D+%7Bm%7D%5E%7B4%7D+%7D+-+sqrt%7B+%7B6%7D%5E%7B2%7D+%7Bm%7D%5E%7B2%7D+%7D+%3D+3m+%2B+2m+-+6m+%3D+-+m)

● Нр.2
![sqrt[4]{625 {c}^{4} } - sqrt[5]{32 {c}^{5} } + sqrt{36 {c}^{2} } = sqrt[4]{ {5}^{4} {c}^{4} } - sqrt[5]{ {2}^{5} {c}^{5} } + sqrt{ {6}^{2} {c}^{2} } = 5c - 2c + 6c = 9c sqrt[4]{625 {c}^{4} } - sqrt[5]{32 {c}^{5} } + sqrt{36 {c}^{2} } = sqrt[4]{ {5}^{4} {c}^{4} } - sqrt[5]{ {2}^{5} {c}^{5} } + sqrt{ {6}^{2} {c}^{2} } = 5c - 2c + 6c = 9c](https://tex.z-dn.net/?f=+sqrt%5B4%5D%7B625+%7Bc%7D%5E%7B4%7D+%7D+-+sqrt%5B5%5D%7B32+%7Bc%7D%5E%7B5%7D+%7D+%2B+sqrt%7B36+%7Bc%7D%5E%7B2%7D+%7D+%3D+sqrt%5B4%5D%7B+%7B5%7D%5E%7B4%7D+%7Bc%7D%5E%7B4%7D+%7D+-+sqrt%5B5%5D%7B+%7B2%7D%5E%7B5%7D+%7Bc%7D%5E%7B5%7D+%7D+%2B+sqrt%7B+%7B6%7D%5E%7B2%7D+%7Bc%7D%5E%7B2%7D+%7D+%3D+5c+-+2c+%2B+6c+%3D+9c)

_________________________________________
Решить уравнение.
● Нр.3.

После проверуи установили, что
х≠0
Ответ: х=9
● Нр.4

После проверуи установили, что
х≠0
Ответ: х=7
● Нр.5.

Ответ: х1=1; х2=2; х3=0; х4=(-3)
● Нр.6.

_________________________________________
● Нр.7

х+7≠0
ОДЗ:
х ≠ -7

● Нр.8.
▪а)

▪б)

● Нр.8.в) на фото у меня не доделано!!!
Исправления напишу здесь, т.к. не получается вставить новое фото. А также напишу второй вариант решения этого задания. Он тебе наверно будет проще.
5^х = 5
х = 1
_____
5^х = 1
5^х = 5^0
х = 0
________
Ответ: х=(1;5)
▪второй способ решения этого задания:
25^х - 6×5^х + 5 < 0
(5^х)^2 - 6×5^х + 5 < 0
заменим: 5^х = у
у^2 - 6у + 5 < 0
D=36 - 4×5 = 36 - 20 = 16
▪y1 = (6+√16)/2 = (6+4)/2 = 10/2 = 5
▪y2 = (6-√16)/2 = (6-4)/2 = 2/2 = 1
обратная замена:
▪5^х = у1
5^х = 5
х = 1
▪5^х = у2
5^х = 1
5^х = 5^0
х = 0
5^х = 5^0
х = 1
● Нр.2
_________________________________________
Решить уравнение.
● Нр.3.
После проверуи установили, что
х≠0
Ответ: х=9
● Нр.4
После проверуи установили, что
х≠0
Ответ: х=7
● Нр.5.
Ответ: х1=1; х2=2; х3=0; х4=(-3)
● Нр.6.
_________________________________________
● Нр.7
х+7≠0
ОДЗ:
х ≠ -7
● Нр.8.
▪а)
▪б)
● Нр.8.в) на фото у меня не доделано!!!
Исправления напишу здесь, т.к. не получается вставить новое фото. А также напишу второй вариант решения этого задания. Он тебе наверно будет проще.
5^х = 5
х = 1
_____
5^х = 1
5^х = 5^0
х = 0
________
Ответ: х=(1;5)
▪второй способ решения этого задания:
25^х - 6×5^х + 5 < 0
(5^х)^2 - 6×5^х + 5 < 0
заменим: 5^х = у
у^2 - 6у + 5 < 0
D=36 - 4×5 = 36 - 20 = 16
▪y1 = (6+√16)/2 = (6+4)/2 = 10/2 = 5
▪y2 = (6-√16)/2 = (6-4)/2 = 2/2 = 1
обратная замена:
▪5^х = у1
5^х = 5
х = 1
▪5^х = у2
5^х = 1
5^х = 5^0
х = 0
5^х = 5^0
х = 1
Приложения:

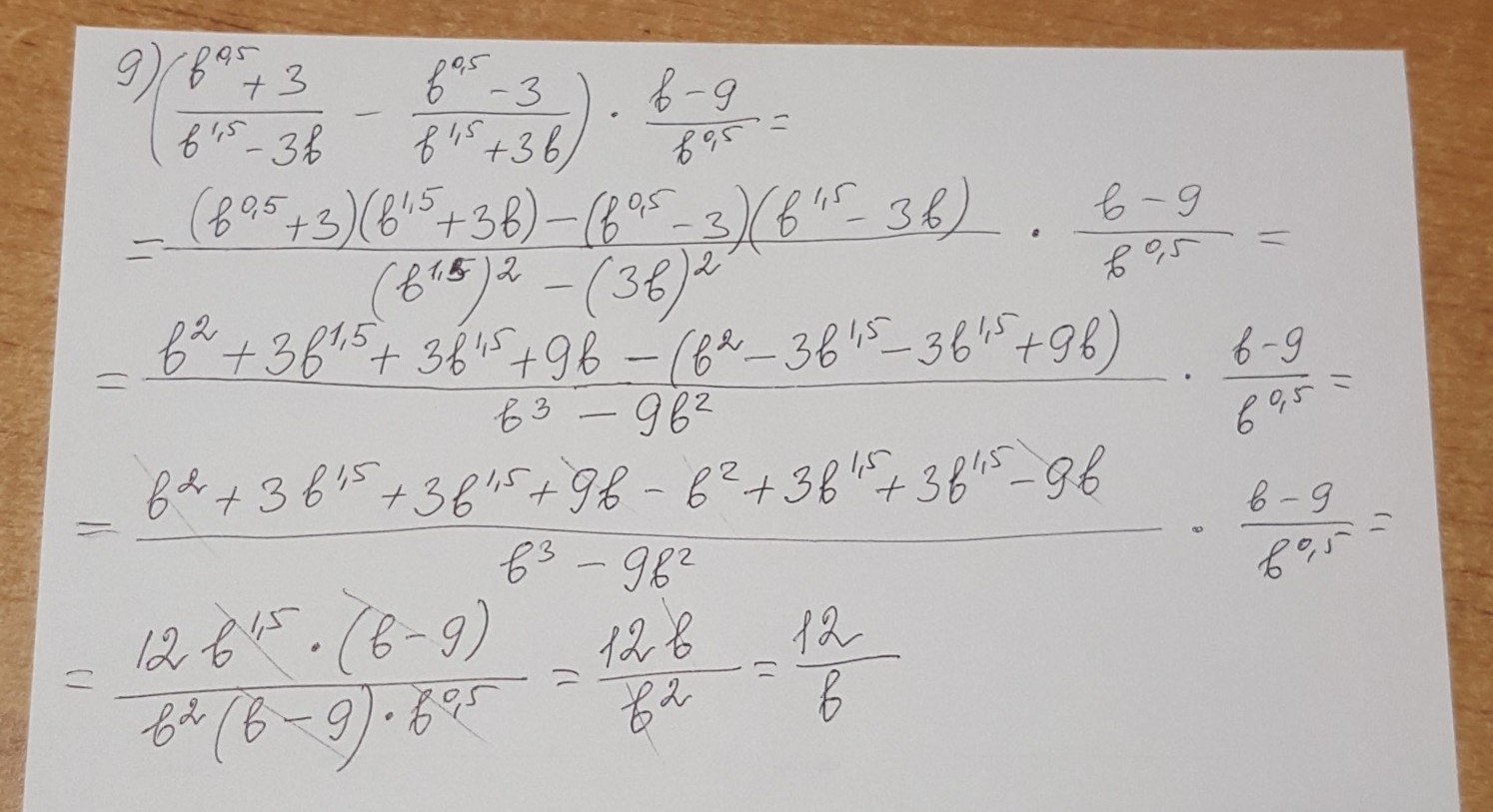
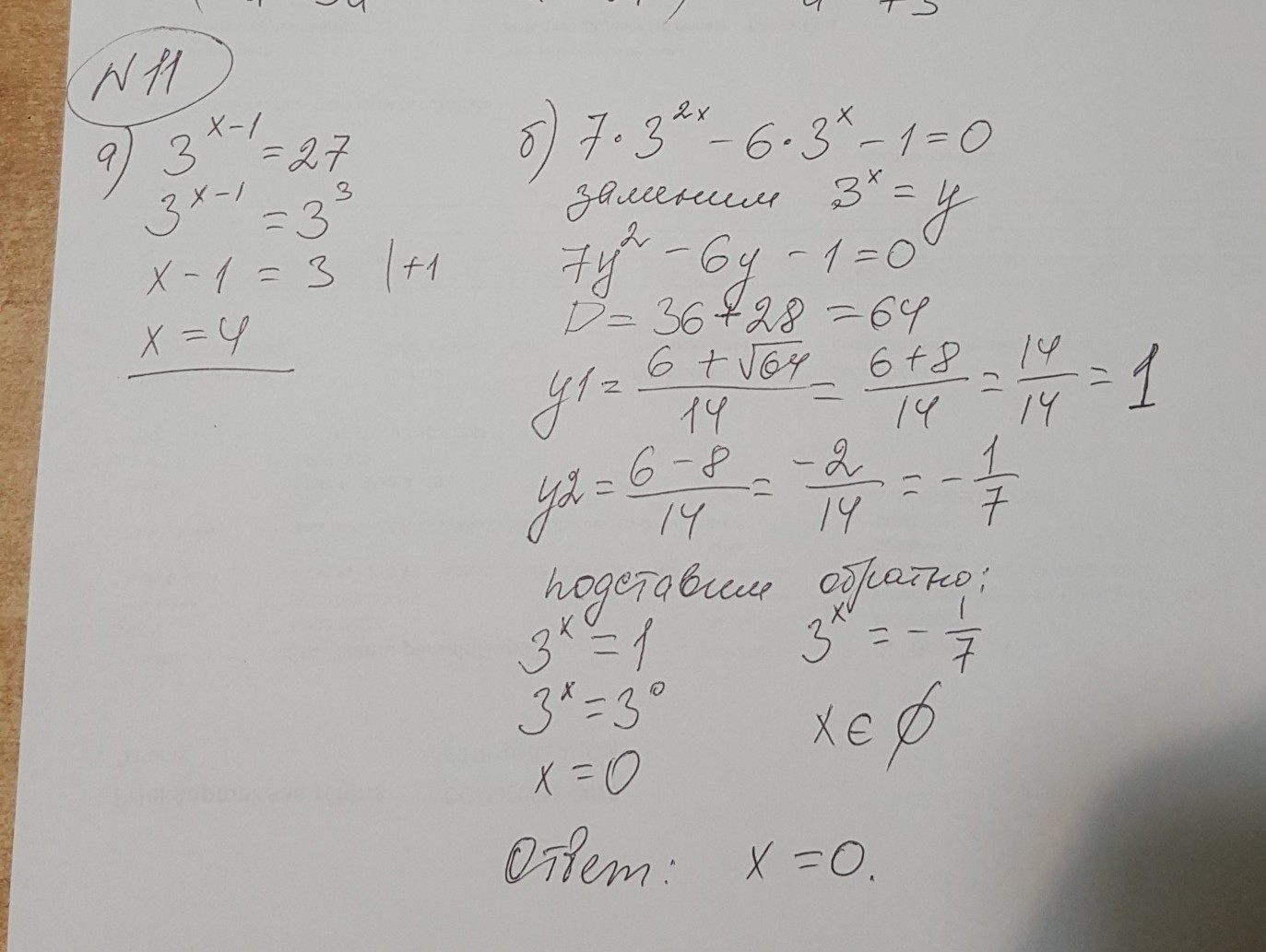
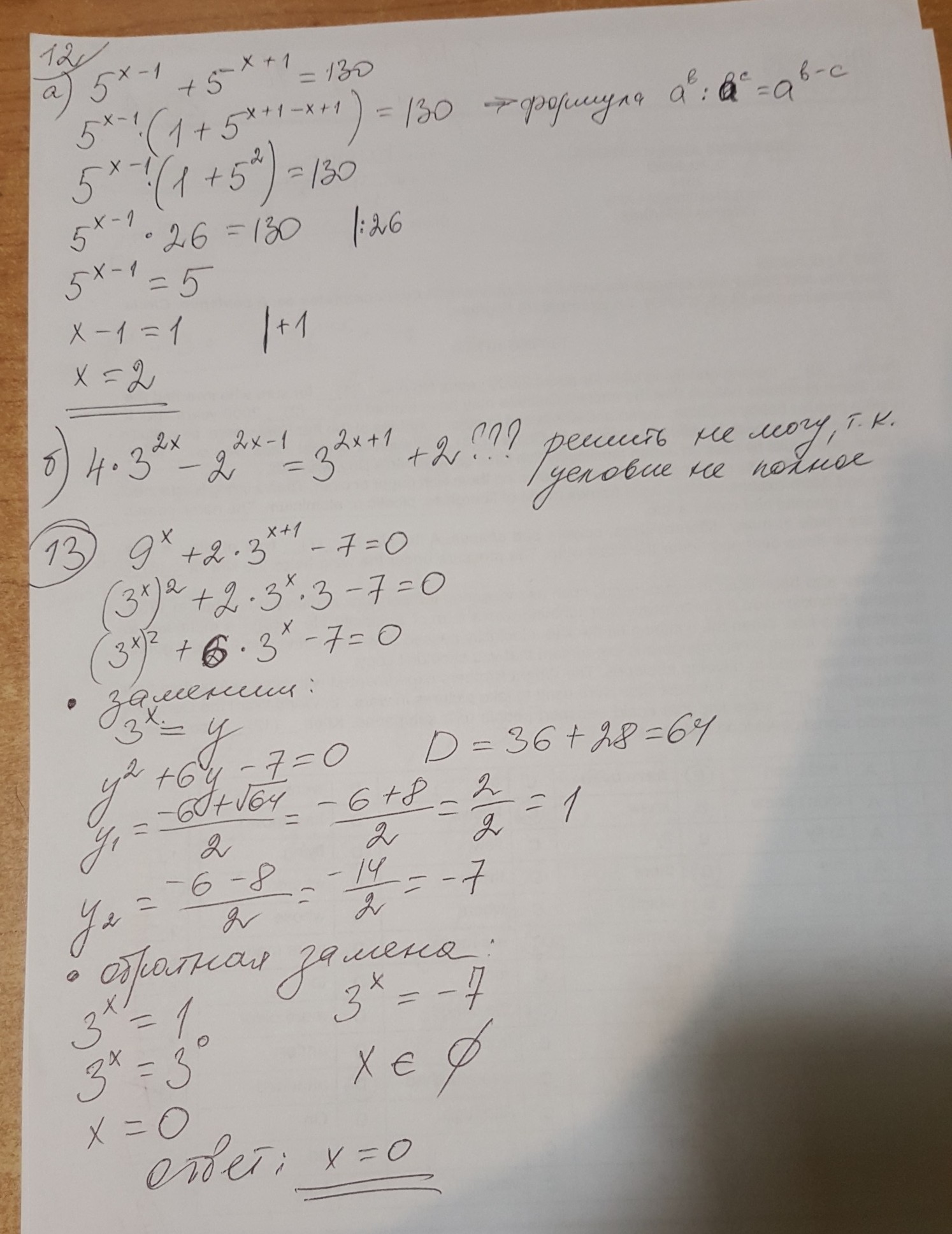
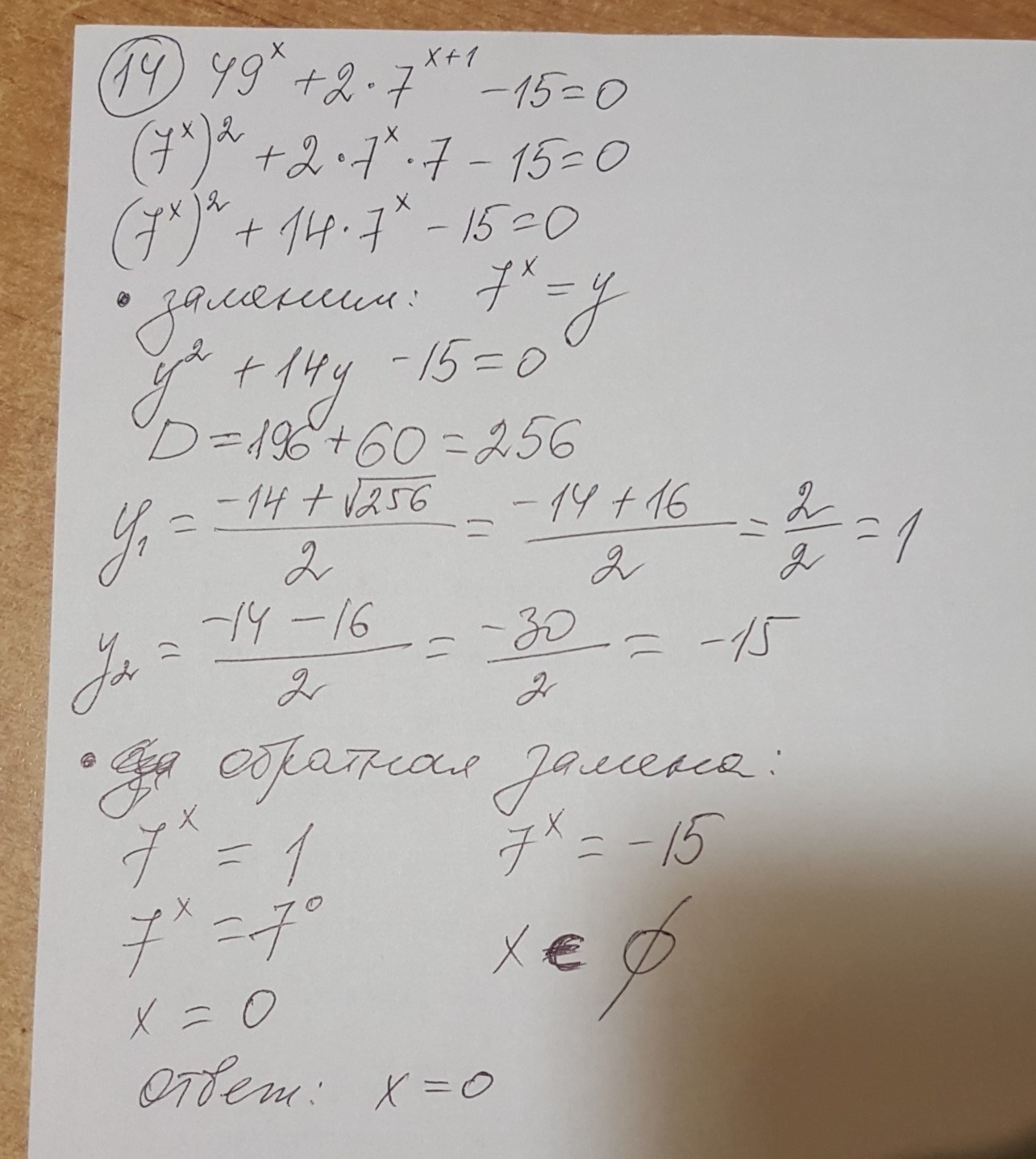
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад



