Ответы
Ответ дал:
0
..............................................................................
Приложения:
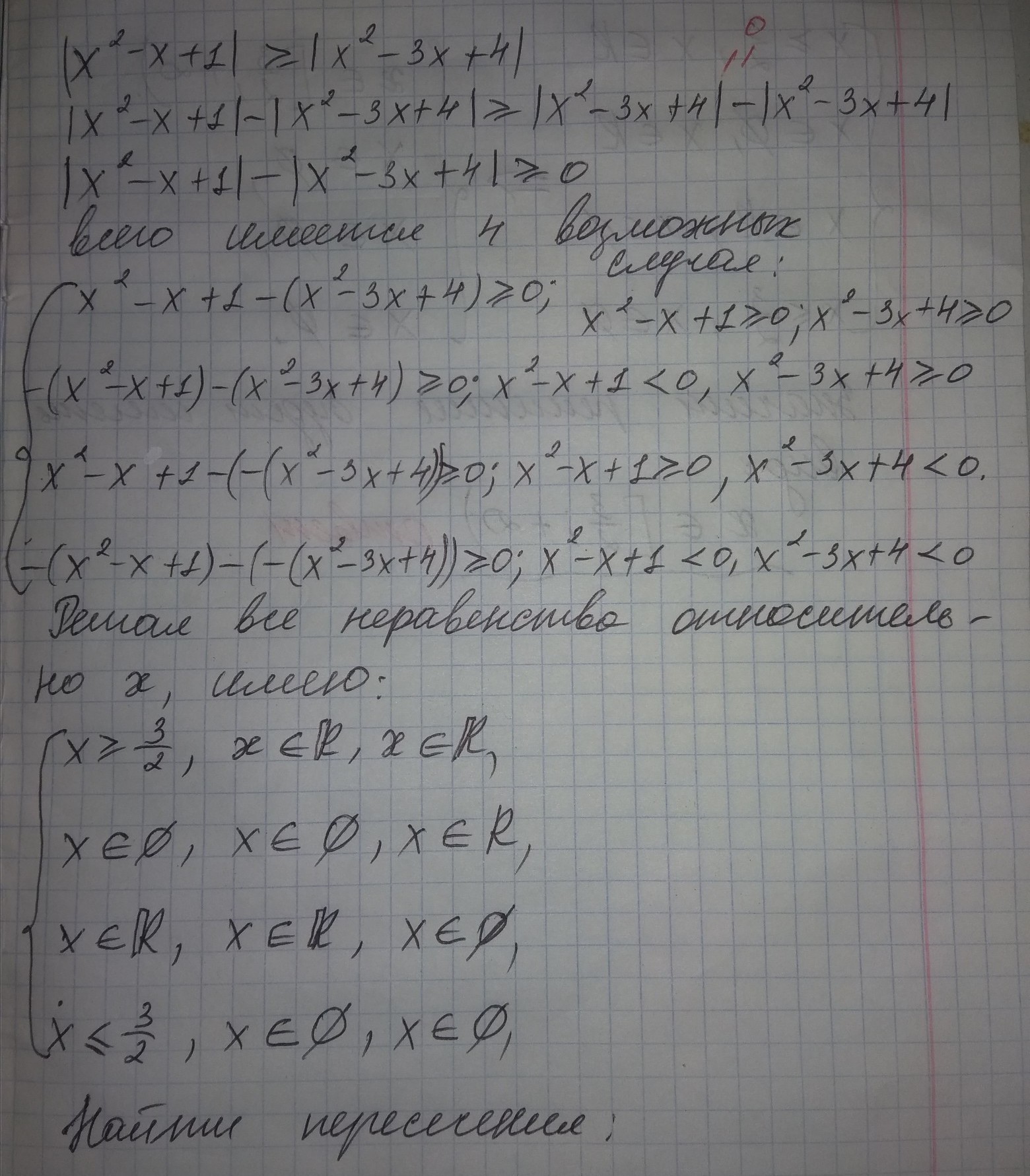
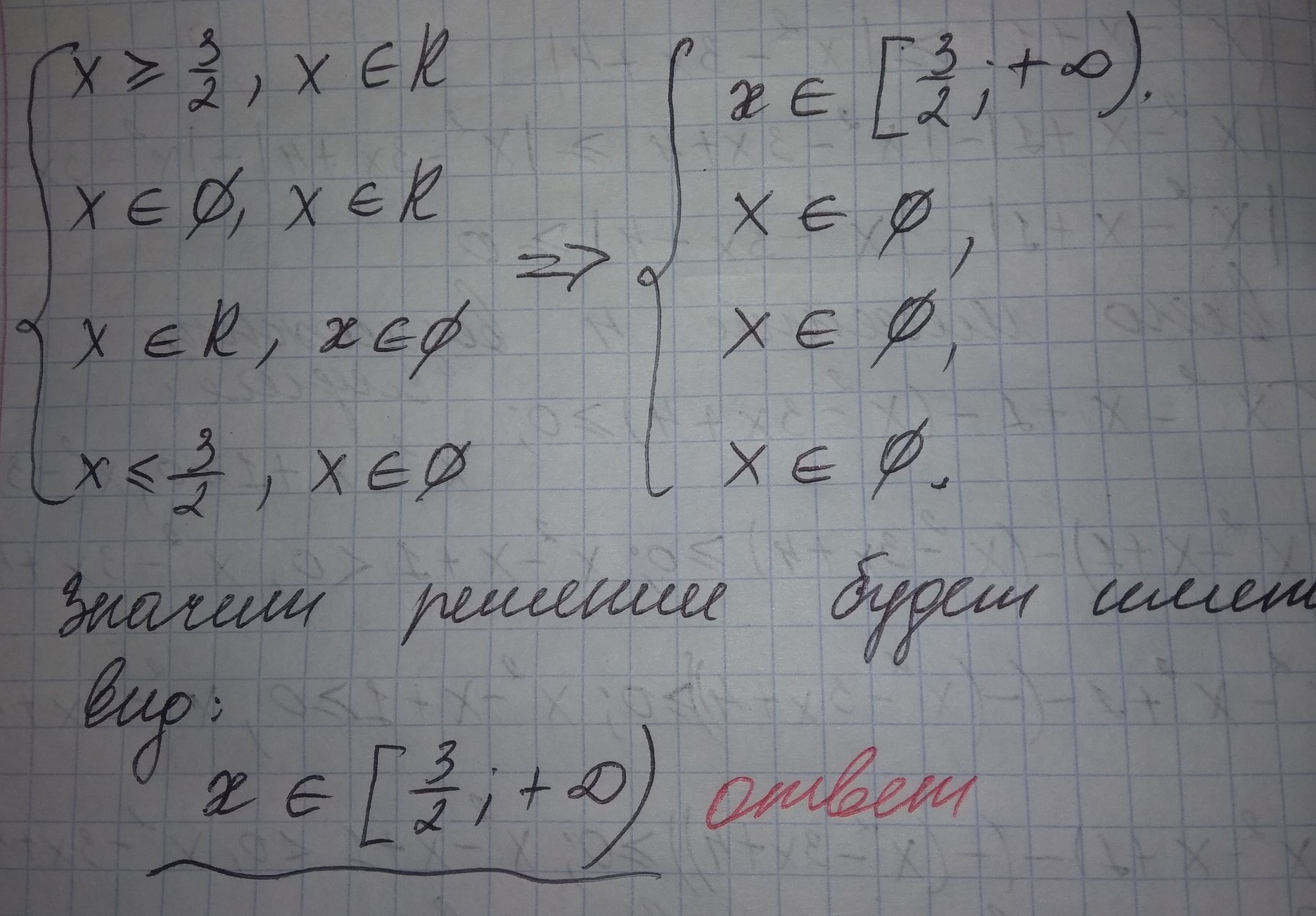
Ответ дал:
0
Спасибо большое за ответ!!!Мне всегда было интересно как можно сделать это с модулем!!Спасибо огромное!!)))
Ответ дал:
0
|x²-x+1|≥|x²-3x+4|
(x²-x+1-(x²-3x+4))•(x²-x+1+x²-3x+4)≥0
(2x-3)(2x²-4x+5)≥0
2x²-4x+5=0
D=16-40=-24<0
2x²-4x+5>0;x(- бес ;+ бес )
2x-3≥0
2x≥3
x≥3/2
x€[3/2;+бес )
|f(x)|≥|g(x)|=>(f(x)-g(x))•(f(x)+g(x))≥0
(x²-x+1-(x²-3x+4))•(x²-x+1+x²-3x+4)≥0
(2x-3)(2x²-4x+5)≥0
2x²-4x+5=0
D=16-40=-24<0
2x²-4x+5>0;x(- бес ;+ бес )
2x-3≥0
2x≥3
x≥3/2
x€[3/2;+бес )
|f(x)|≥|g(x)|=>(f(x)-g(x))•(f(x)+g(x))≥0
Приложения:
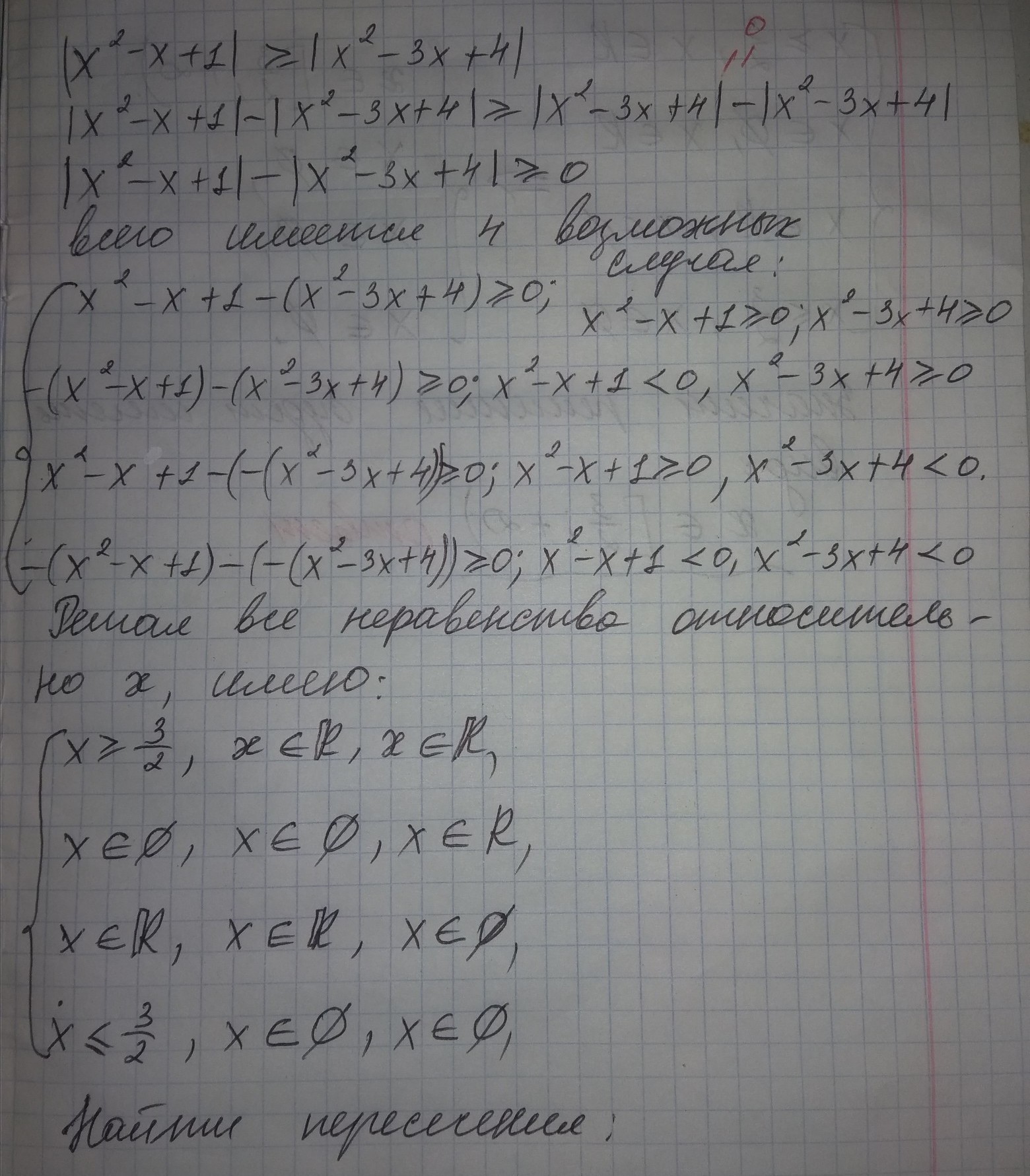
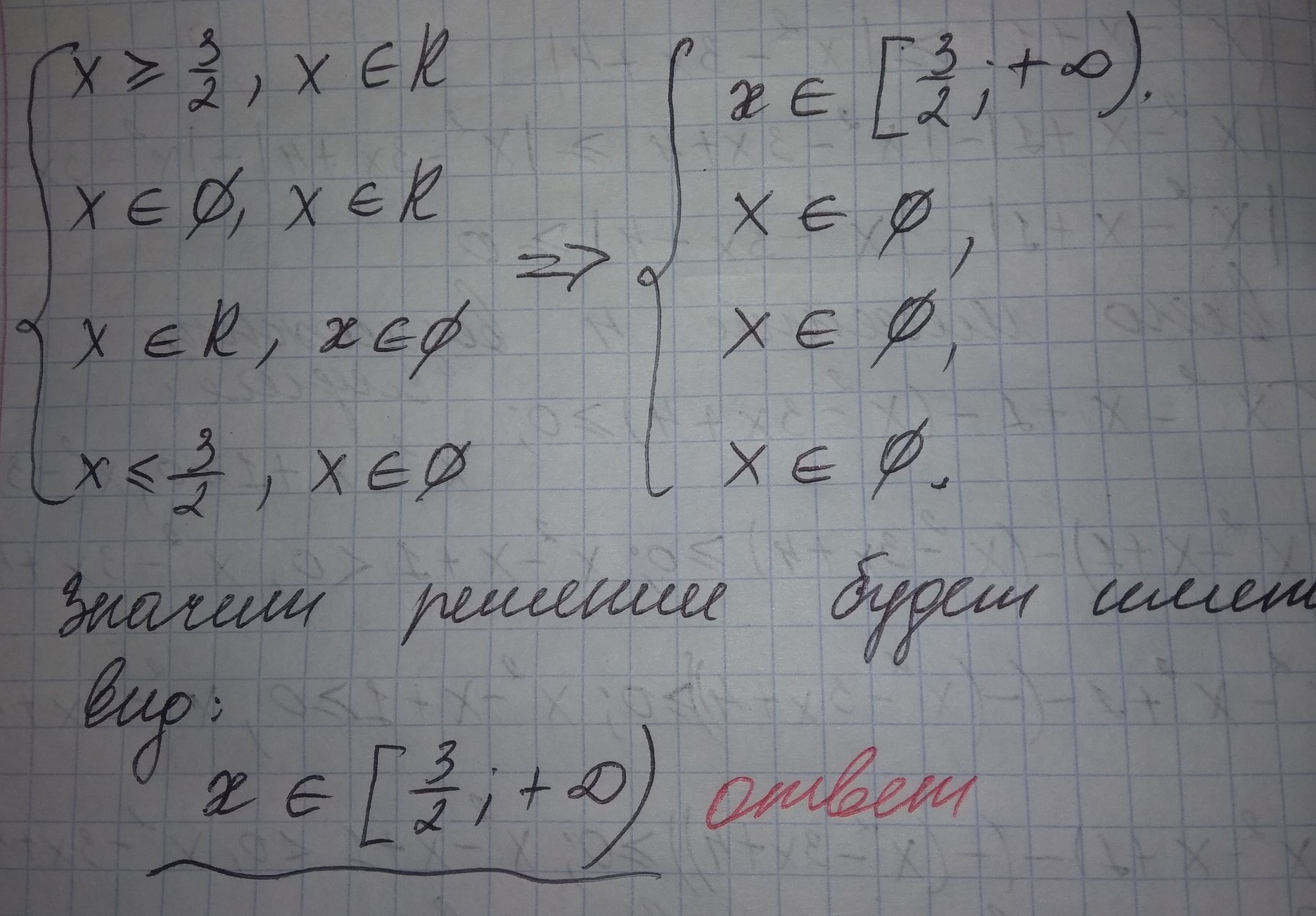
Ответ дал:
0
Так понятно)
Ответ дал:
0
Этот метод рассматривается даже в базовой школе. Во всём должен быть здравый смысл. Ход решения и все шаги решения обоснованы. Уж если говорить по поводу оформления, то единицы пользователей верно оформляют решение, применяя метод интервалов. И молчок. А здесь вдруг недовольство. Спасибо автору ответа за то, что этот способ предложен и рассмотрен.
Ответ дал:
0
А вот допустим мне не понятно как автор решил это уравнение. Вдруг я это еще не проходил. Поэтому при решении надо хотя бы сказать, что за свойство применил отвечающий "Метод рационализации" - "Аааа, понятно".
Ответ дал:
0
Просто как пояснение и всё.
Ответ дал:
0
"А вот допустим" нигде в своих решениях Вы не обосновывает при решении логарифмических неравенств переход к линейным. Нигде нет ни слова об основаниях и свойствах функций. А так бы хотелось их видеть. И уж это точно ошибка (отсутствующая часть обоснований). Так что ещё раз утверждаю: да, нужны обоснования и пояснения, но в рамках разумного. Это моё личное мнение.
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
