Question

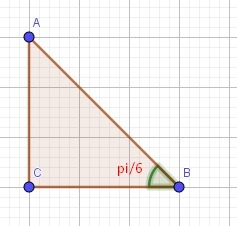
В прямоугольный треугольник,один из углов которого равен $pi /6$,случайным образом бросается точка.Какова вероятность того,что она окажется внутри вписанной в треугольник окружности?

Answer 1

.......................

Answer 2

Пусть гипотенуза АВ = а, тогда против угла 30°, катет АС в два раза меньше за гипотенузу, то есть: $AC=frac{a}{2}$ и тогда по т. Пифагора:

$BC=sqrt{AB^2-AC^2} =sqrt{a^2-(frac{a}{2} )^2} =frac{asqrt{3}}{2}$

Радиус вписанной окружности в прямоугольный треугольник:

$r=dfrac{AC+BC-AB}{2}=frac{frac{a}{2} +frac{asqrt{3}}{2}-a }{2} =frac{a(sqrt{3}-1)}{4}$

Площадь круга вписанного в прямоугольный треугольник, равна:

$S_1=pi r^2=pi cdot(frac{a(sqrt{3}-1)}{4} )^2=pi cdotfrac{a^2(4-2sqrt{3})}{16}=frac{pi a^2(2-sqrt{3})}{8}$

Площадь прямоугольного треугольника:

$S_1=dfrac{ACcdot BC}{2} =dfrac{frac{a}{2}cdotfrac{asqrt{3}}{2}}{2} =dfrac{a^2sqrt{3}}{8}$

Искомая вероятность: $P=dfrac{S_1}{S_2}=dfrac{frac{pi a^2(2-sqrt{3})}{8} }{frac{a^2sqrt{3}}{8}} =dfrac{pi(2-sqrt{3})}{sqrt{3}}=dfrac{pi(2sqrt{3}-3)}{3}$