Question

помогите пожалуйста 258....

Answer 1

В прямоугольном треугольнике катет, лежащий против угла 30°, равен половине гипотенузы. Пусть ВС = х, тогда АВ = 2х.

Найдем АС по теореме Пифагора:

$AC=sqrt{AB^2-BC^2}= sqrt{(2x)^2-x^2}=sqrt{4x^2-x^2}=sqrt{3x^2}=xsqrt{3}$ (см)

Формула радиуса окружности, вписанной в прямоугольный треугольник:

$r=cfrac{a+b-c}{2}$, где а, b - катеты, с - гипотенуза. Отсюда:

$cfrac{AC+BC-AB}{2}=sqrt{3} \\ cfrac{xsqrt{3}+x-2x}{2}=sqrt{3} \ xsqrt{3}-x=2sqrt{3} \\ x(sqrt{3}-1)=2sqrt{3}\\ x=cfrac{2sqrt{3}}{sqrt{3}-1} = cfrac{2sqrt{3}(sqrt{3}+1)}{(sqrt{3}-1)(sqrt{3}+1)} = cfrac{6+2sqrt{3}}{3-1} =cfrac{2(3+sqrt{3})}{2} =3+sqrt{3}$

ВС = 3+√3 (cм)

АС = х√3 = (3+√3)√3 = 3√3 + 3 (см)

$S_{ABC}=cfrac{1}{2} cdot AC cdot BC =cfrac{(3sqrt{3}+3)(3+sqrt{3})}{2} = cfrac{9sqrt{3}+9+9+3sqrt{3}}{2} = \\=cfrac{12sqrt{3}+18}{2} =cfrac{2(6sqrt{3}+9)}{2} =6sqrt{3}+9$

Ответ: 6√3+9 см²

Answer 2

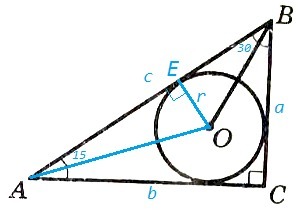
AO, BO - биссектрисы

E - точка касания на AB, OE⊥AB

AB= c, OE= r =√3

AE= ctg15 *r

BE= ctg30 *r

sin15= sin(45-30) = √2/2 ·√3/2 -√2/2 ·1/2 =(√6-√2)/4 =(√3-1)/2√2

ctg15 +ctg30= sin45/sin15sin30 = √2/2 ÷ 1/2 ÷ (√3-1)/2√2 =4/(√3-1) =2(√3+1)

c= AE+BE = r(ctg15 +ctg30) = r*2(√3+1)

r= (a+b-c)/2 <=> (a+b+c)/2 = r+c

S= r*(a+b+c)/2 = r(r+c) = r^2 +r^2*2(√3+1) = r^2*(3+2√3) =9 +6√3 (см^2)  ~19,39