Ответы
Ответ дал:
0
Приложения:
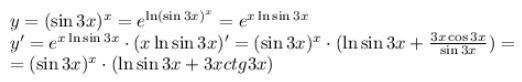
Ответ дал:
0
как я об этом узнаю?
Ответ дал:
0
1 вопрос. Там у нас (sin3x)^x в конце тоже остался. Это как?
Ответ дал:
0
Степенно-показательное выражение (sin3x)^x представляем через экспоненту е, т.к. ее производная известна. Причем (e^t)'=e^t·t' (производная сложной функции). Поэтому далее эта экспонента возвращается в исходный вид.
Ответ дал:
0
Ну теперь понял. Спасибо. Есть ВК
Ответ дал:
0
Если можно дайте пж?
Ответ дал:
0
Можно также применить логарифмическое дифференцирование:
Приложения:

Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад