Question

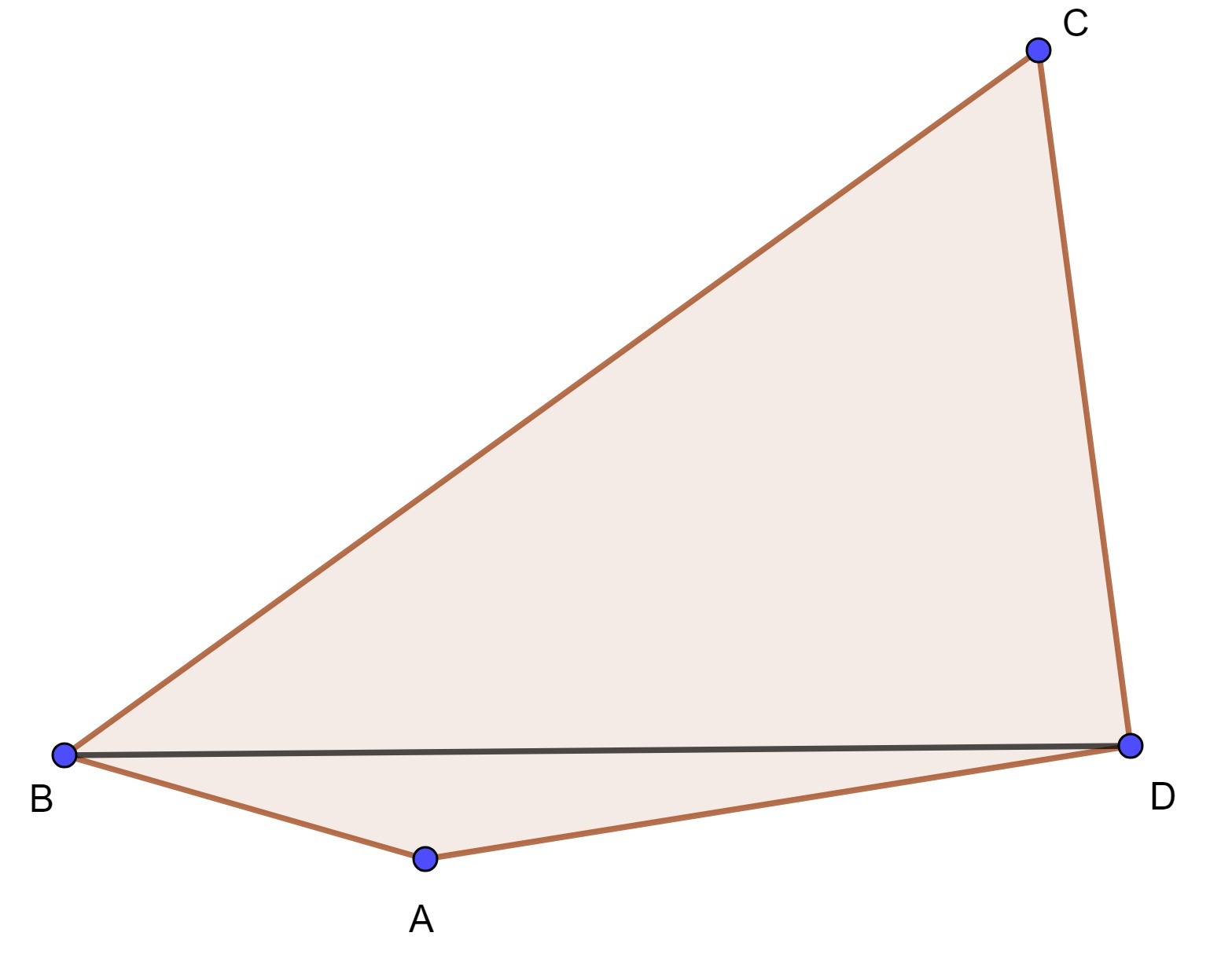
В четырехугольнике ABCD внешний угол при вершине А равен углу BCD, AD=CD. Докажите, что BD — биссектриса

Answer 1

Пусть внешний угол при вершине A равен α. Тогда угол BCD = α, а угол BAD равен 180°-α. Заметим, что сумма противоположных углов равна 180°-α+α = 180°; Значит данный четырехугольник можно вписать в окружность. Пусть ее радиус равен R; По теореме синусов: $AD=2Rsin angle ABD$ и $CD = 2Rsin angle DBC$, поскольку AD = CD, то углы ABD и DBC равны, а значит, BD - биссектриса

Answer 2

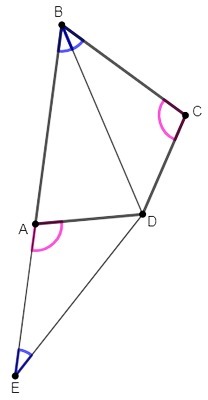
На луче BA отложим отрезок AE равный BC.

AE=BC, ∠EAD=∠BCD, AD=CD

△EAD=△BCD (по двум сторонам и углу между ними), ∠AED=∠CBD, ED=BD

△BDE - равнобедренный, ∠AED=∠ABD

∠ABD=∠CBD, BD- биссектриса ∠ABC