Ответы
Ответ дал:
0
5/(25+5ˣ)≤4/((0,2)⁻ˣ-5)
5/(25+5ˣ)≤4/((1/5)⁻ˣ-5)
5/(25+5ˣ)≤4/(5ˣ-5)
ОДЗ:
Так как 5/(25+5ˣ)>0 ⇒
4/(5ˣ-5)>0
5ˣ-5>0
5ˣ>5
x>1
5*(5ˣ-5)≤4*(25+5ˣ)
5*5ˣ-25≤100+4*5ˣ
5ˣ≤125
5ˣ≤5³
x≤3 ⇒
Согласно ОДЗ:
Ответ: x∈(1;3].
2*sinx*cosx+4*cosx+sinx+2=0
2*cosx*(sinx+2)+(sinx+2)=0
(sinx+2)*(2*cosx+1)=0
sinx+2=0
sinx=-2 ∉ так как |sinx|≤1.
2*cosx+1=0
2*cosx=-1
cosx=-1/2 ⇒
Ответ: x₁=2π/3 x₂=4π/3.
Ответ дал:
0
не верно первый номер
Ответ дал:
0
5/(25+5ˣ)>0 при любом x ⇒ так как 5/(25+5ˣ)≤4/(5ˣ-5), то 4/(5ˣ-5)>0 ⇒ x>1 - отсутствующий у вас кусок ОДЗ
Ответ дал:
0
решение на фото внизу
Приложения:
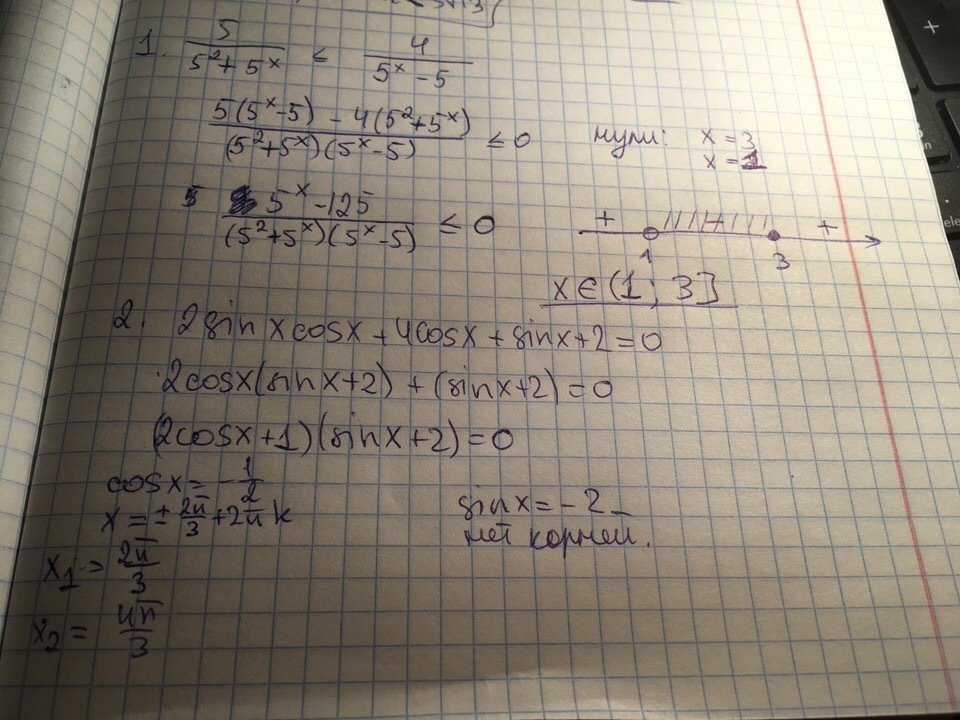
Ответ дал:
0
А решения первого нет?(
Ответ дал:
0
на фото оба задания
Ответ дал:
0
Ой,всё,сори,я затупил.
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
