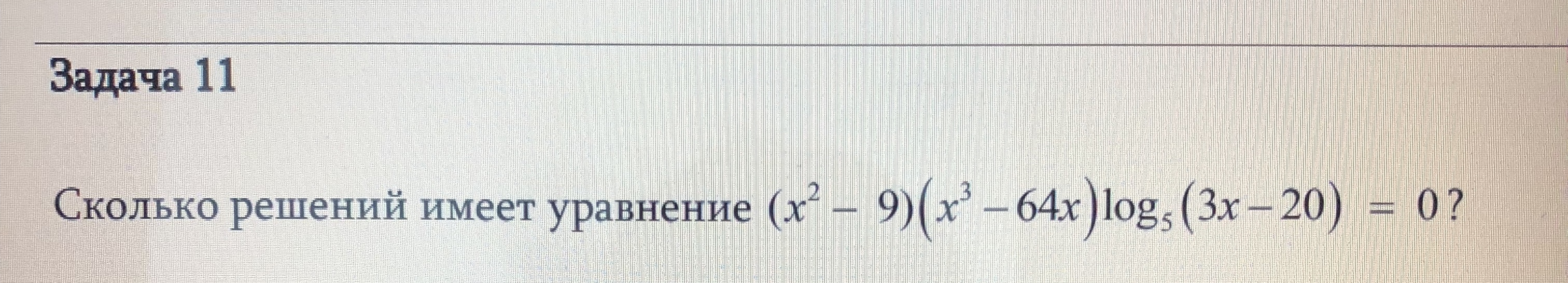Question

Сколько решений имеет уравнение?

Answer 1

Разложим на множители
$(x-3)(x+3) x (x-8)(x+8) log_5 (3x-20)=0$
Уравнение равно нулю, если хотя бы один из сомножителей равен нулю, а другие при этом не теряют смысла.
x-3=0 или x+3=0 или x=0 или x-8=0 или x+8=0 или
$Log_5 (3x-20)=0$
Решаем каждое уравнение в отдельности
x=3; x= -3; x=0; x=8; x= -8;

$log_5 (3x-20)=log_51\ 3x-20=1\3x=21\x=7$. 

Одз: 3x-20> 0; 3x> 20; x> $6 frac{2}{3}$

Значит,  -3; 3; 0 и -8 не являются корнями

Итого получаем: 2 корня имеет уравнение

Answer 2

Забыли про область определения логарифма. Решений меньше.

Answer 3

Спасибо

Answer 4

Уравнение имеет 2 решения.
Более подробно - на фото.
Не забывайте про область определения