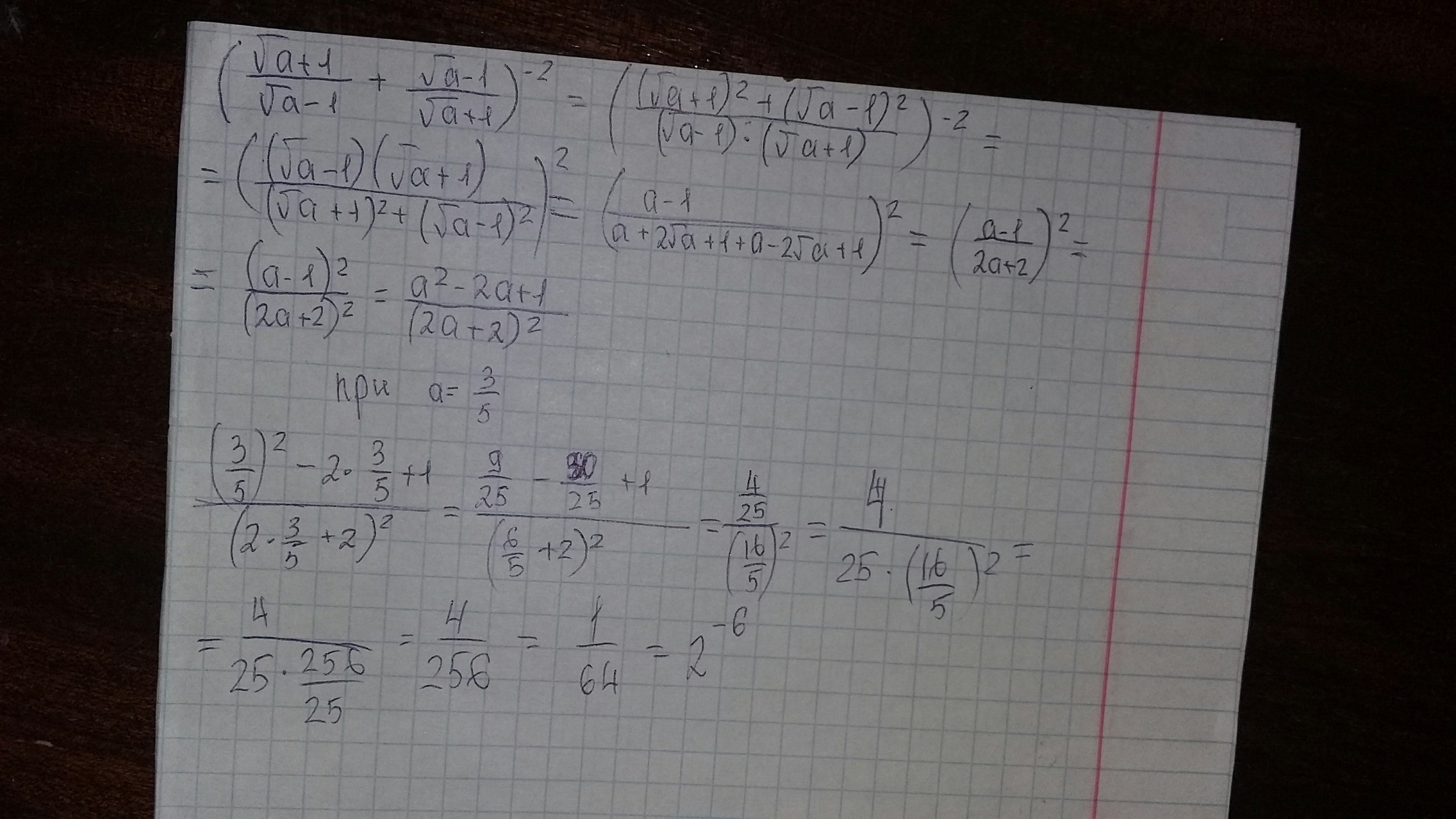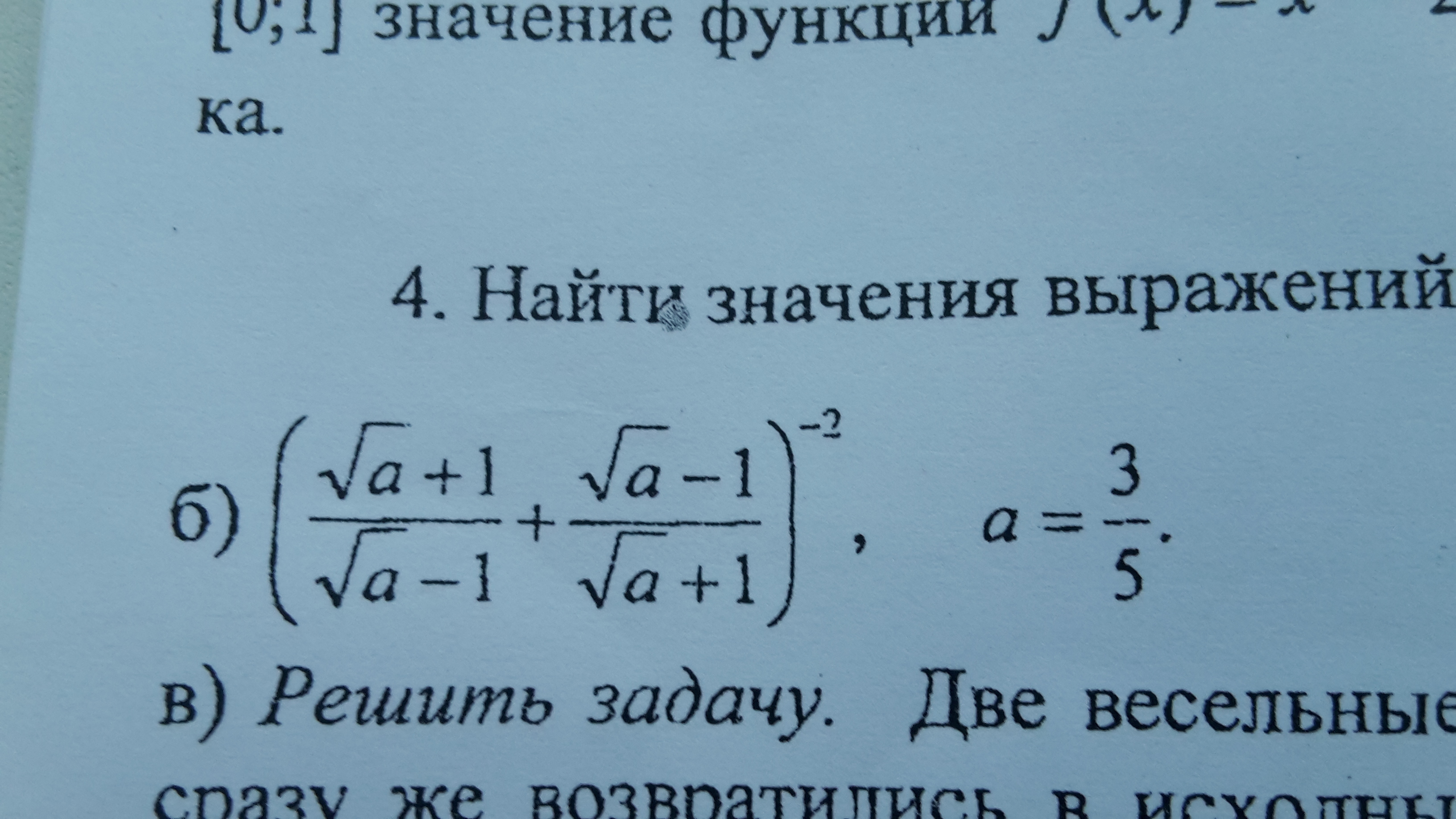Question

Пожалуйста, помогите, не помню и все на этом....

Answer 1

Решение на фотографии

_____________________

Answer 2

Спасибо большое!

Answer 3

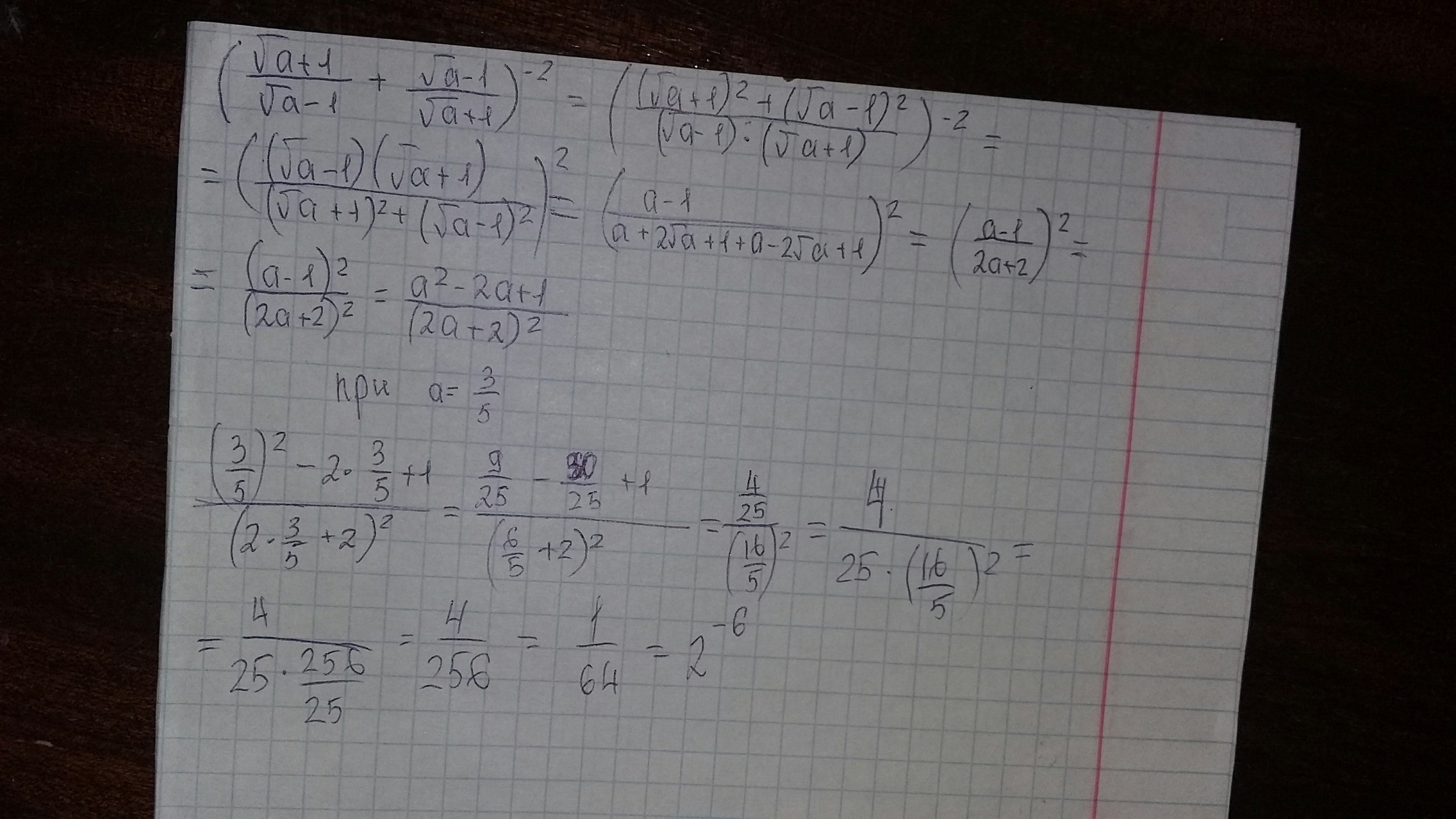
Сначала выражение нужно упростить. Будем делать это по частям: сначала приведем к общему знаменателю и упростим выражение внутри скобок, потом возведем в степень.

1) Упрощение выражения внутри скобок: приводим к одному знаменателю, для этого умножаем и числитель, и знаменатель первой дроби на (√a + 1), второй – на (√a - 1), благодаря чему можем записать данные дроби под общей дробной чертой. Раскрываем числитель по формуле сокращенного умножения (a + b)² = a² + 2ab + b², (a - b)² = a² - 2ab + b², знаменатель по такой: a² - b² = (a - b)(a + b).

$frac{sqrt{a} + 1}{sqrt{a} - 1 } + frac{sqrt{a} - 1}{sqrt{a} + 1} = frac{(sqrt{a} + 1)^2 + (sqrt{a} - 1)^2 }{(sqrt{a} - 1)(sqrt{a} + 1)} = frac{a + 2sqrt{a} + 1 + a - 2sqrt{a} + 1}{a - 1} = frac{2a + 2}{a - 1} = frac{2(a + 1)}{a - 1}$

2) Возводим полученное в (-2) степень: возведение в отрицательную значит переворот дроби (числитель становится знаменателем и наоборот), вторая – квадрат:

$(frac{2(a + 1)}{a - 1})^{-2} = (frac{a - 1}{2(a + 1)})^2 = (frac{0,6 - 1}{2 * 1,6})^2 = (frac{-0,4}{3,2})^2 = (frac{-4}{32})^2 = (frac{-1}{8})^2 = frac{1}{64} = 2^{-6}.$

Ответ: $2^{-6}.$