Question

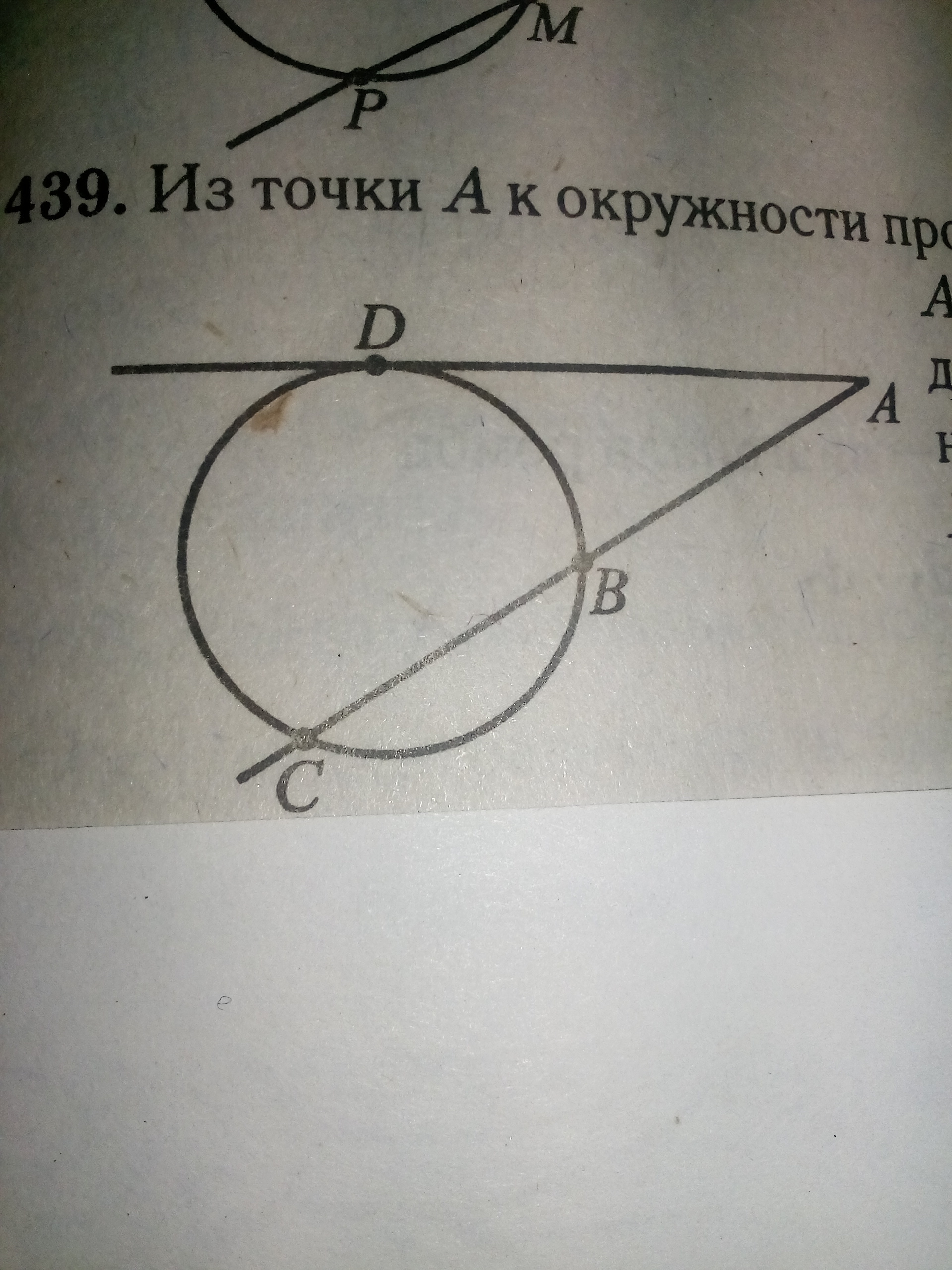
Из точки А к окружности проведены касательная и секущая. АД=12, длина отрезка АВ больше длины отрезка ВС на 2. Найдите длину меньшего отрезка, на которые точка В делит отрезок АС

Answer 1

По теореме о касательной и секущей: $AD^{2}=ABtimes AC$; Пусть AB=x; $144=x(2x-2) Leftrightarrow 72=x^{2}-x Leftrightarrow x=9$;

BC - меньший отрезок. BC = 9-2=7;

Ответ: 7