Question

Свойства арифметической прогрессии

Answer 1

1)

Решение:

a1=41

d=1

?-65

an=a1+(n-1)d

65=41+n-1

n=65-41+1

n=25

Значит a25=65.

$Sn=frac{a1+an}{2}*n=frac{41+65}{2}*25=frac{106}{2}*25=53*25= 1325$

Ответ: сумма натуральных чисел от 41 до 65 равна 1325.

2)

Дано:

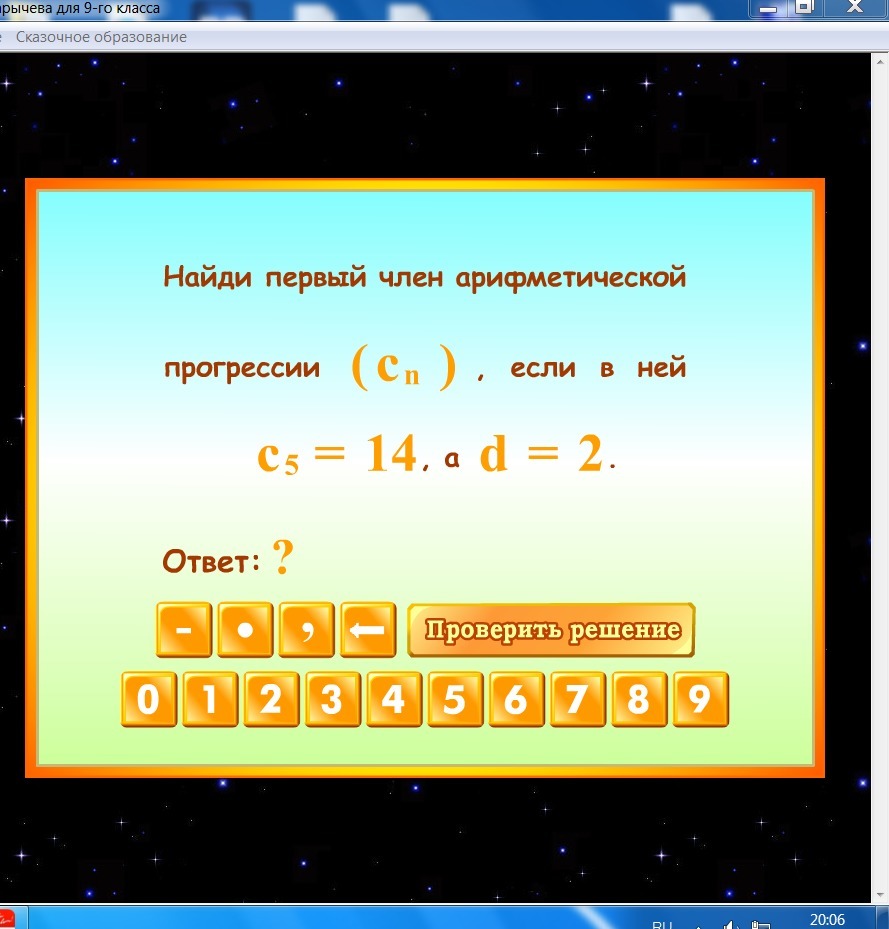
с5=14

d=2

c1-?

сn=c1+(n-1)d

Находим первый член арифметической прогрессии по (c5):

c5=c1+4d

14=c1+4×2

c1=14-8

c1=6.

Ответ: первый член арифметической прогрессии равен (c1)=6.

Answer 2

$mathtt{n=65-41+1=25;~S_{25}=frac{41+65}{2}*25=53*25=1325}$

$mathtt{d=frac{a_n-a_k}{n-k}}$, следовательно, $mathtt{a_k=a_n-d(n-k)}$; в нашем же случае, $mathtt{c_1=c_5-2(5-1)=14-2*4=6}$