Ответы
Ответ дал:
0
f'(x)=4*3x^3-12x^2=12x^3-12x^2
f'(x)=0
12x^2(x-1)=0
x=0
x=1
12x^2(x-1)v0 (v - знак сравнения меньше, больше, не важно)
(см. рисунок)
точка 1 - это минимум, точка 0 не является точкой экстремума
Ответ: {}
Приложения:
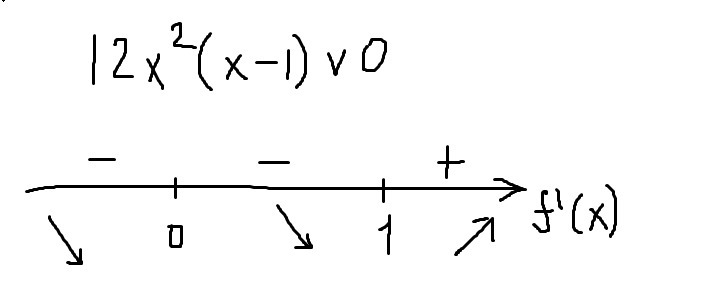
Ответ дал:
0
вы нашли точку минимума
Ответ дал:
0
а просили максимум функции
Ответ дал:
0
да, ошибка
Ответ дал:
0
уб уб возр
_(0)_(1)_
"-" "-" "+"
функция точек максимума не имеет, соответственно максимума у нее нет.
Ответ: ∅
Приложения:
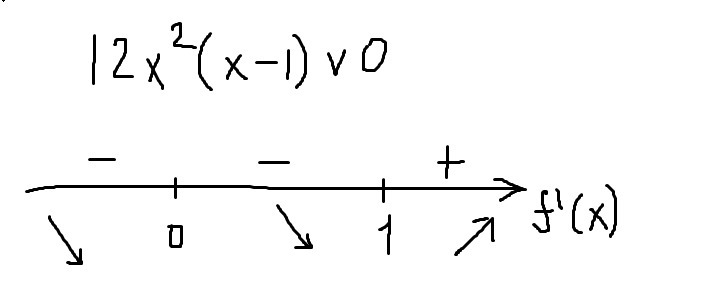
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
10 лет назад
10 лет назад
