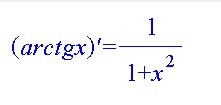Ответы
Ответ дал:
0
Если f(x) и g(x) - обратные, то . Тогда имеем следующее следствие:
Положим . Имеем
Ответ дал:
0
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад