Ответы
Ответ дал:
0
Раз ничего не сказано сколько решить - возьму только седьмое задание.
Поскольку левая и правая части уравнения принимают неотрицательные значения, то возводим оба части уравнения в квадрат:
И задание восьмое:)
Ответ дал:
0
1)

Ответ: 4)
2)

Ответ: 1)
3)

Ответ: 1)
4)

Ответ: 1)
6)

ОДЗ:

(-беск; -2sqrt(2)) U (2sqrt(2); + беск)
оба корня удовл.одз.
Ответ: 2)
7)

Ответ: 4)
8)

Ответ: 1)
5)

дальше во вложении.
Наибольшее по модулю целое решение -- |-1| = 1
Ответ: 1)
Ответ: 4)
2)
Ответ: 1)
3)
Ответ: 1)
4)
Ответ: 1)
6)
ОДЗ:
(-беск; -2sqrt(2)) U (2sqrt(2); + беск)
оба корня удовл.одз.
Ответ: 2)
7)
Ответ: 4)
8)
Ответ: 1)
5)
дальше во вложении.
Наибольшее по модулю целое решение -- |-1| = 1
Ответ: 1)
Приложения:
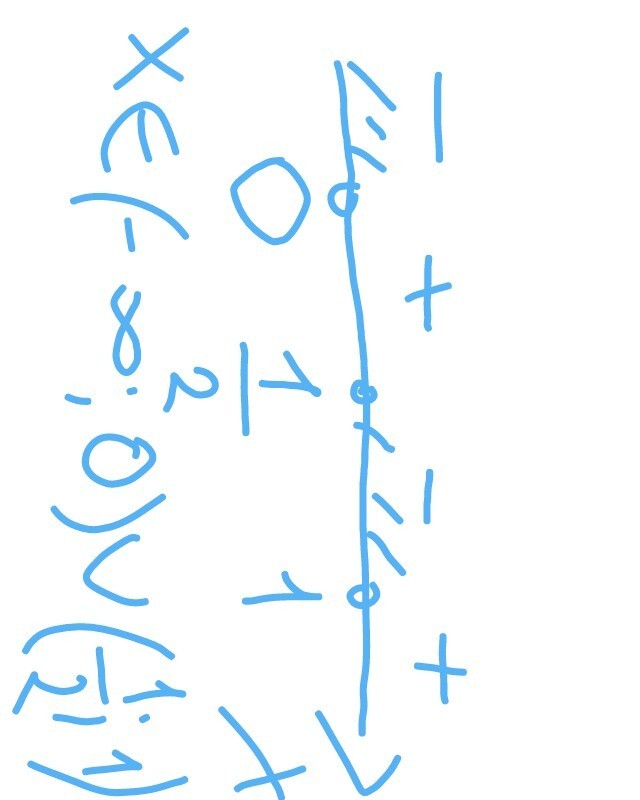
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад
10 лет назад
