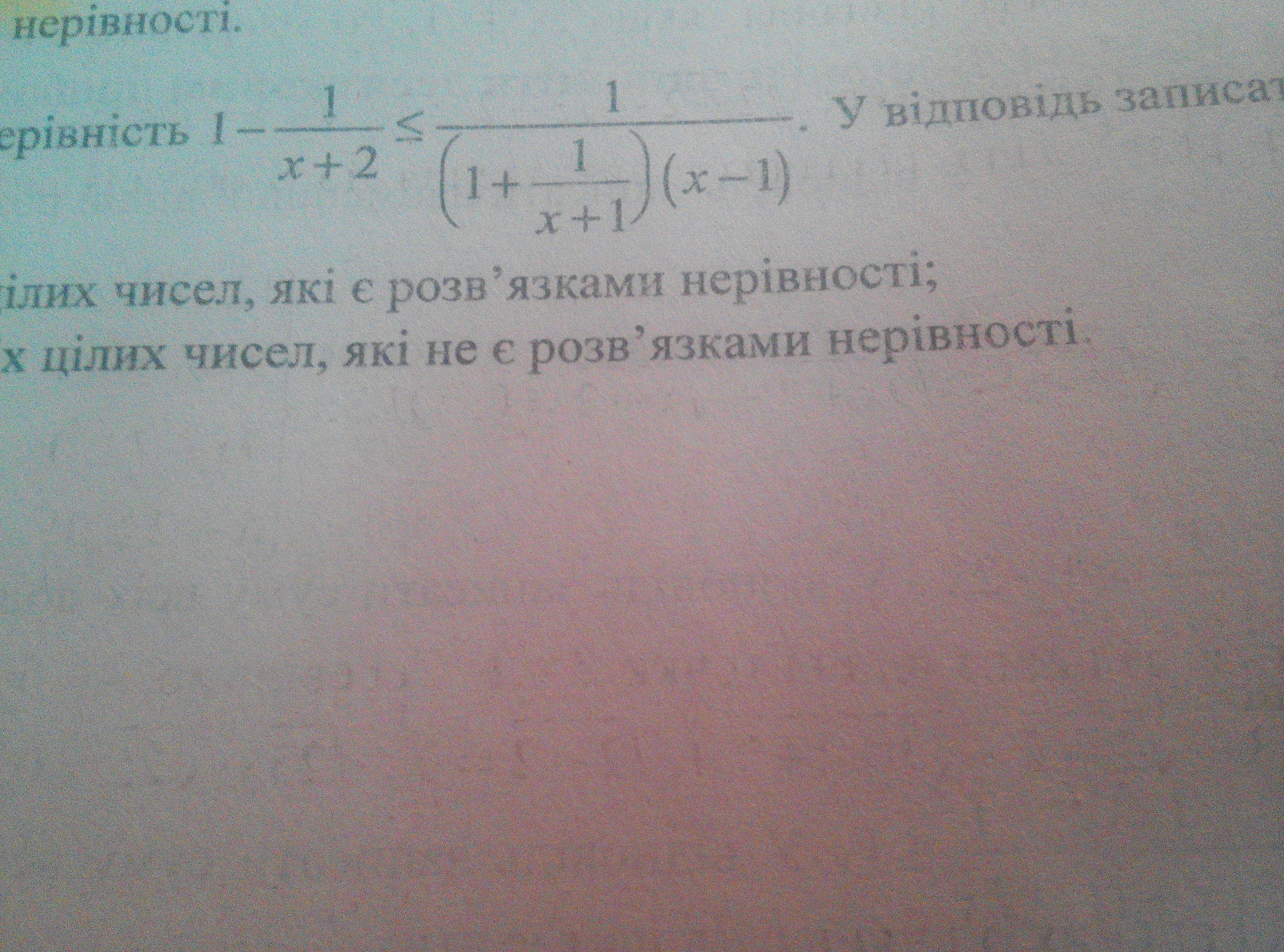Ответы
Ответ дал:
0
Продолжение решения во вложении.
Приложения:

Ответ дал:
0
Посмотрите поподробнее. Вы ОДЗ потеряли!
Ответ дал:
0
Где?
Ответ дал:
0
Вначале: -1 не включена
Ответ дал:
0
Ах, да, всё, увидел
Ответ дал:
0
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Приложения:




Вас заинтересует
2 года назад
3 года назад
9 лет назад
9 лет назад