Question

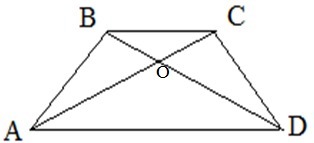
О-точка перетину діагоналей трапеції ABCD з основами AD і BC; BO=6 см, OD= 9 см. Знайдіть довжину меншої з основ трапеції, якщо її середня лінія дорівнює 10см.

Answer 1

1) $angle AOD=angle COB$ как вертикальные.

2) $angle DAO=angle BCO$ как внутренние накрест лежащие при $AD || BC$ и секущей $AC$

Таким образом, треугольники $AOD$ и $COB$ подобные (по двум углам).

Из подобия треугольников: $displaystyle frac{AD}{BC}=dfrac{OD}{OB}$

Пусть MN - средняя линия трапеции(на рисунке не нарисовал); MN=10 см

$MN=dfrac{AD+BC}{2}=10~~~Rightarrow~~~ AD=20-BC$

Подставим в соотношение: $displaystyle frac{20-BC}{BC}=frac{9}{6}~~~Rightarrow~~~frac{20}{BC}-1=frac{3}{2} \ \ frac{20}{BC}=frac{5}{2}~~~Rightarrow~~ boxed{BC=frac{40}{5}=8~cm}$

Ответ: 8 см.